When forces F1 , F2 , F3 are acting on a particle of mass m such that F2 and F3 are mutually prependicular, then the particle remains stationary. If the force F1 is now rejmoved then the acceleration of the particle is
F1/m
F2F3/mF1
F2−F3/m
F2/m
The correct Answer is:a
To solve the problem step by step, we can follow the reasoning laid out in the video transcript:
Step 1: Understand the Forces Acting on the Particle
We have three forces acting on a particle of mass m: F1, F2, and F3. It is given that F2 and F3 are mutually perpendicular.
Step 2: Condition for the Particle to be Stationary
For the particle to remain stationary, the net force acting on it must be zero. This can be expressed mathematically as:
F1+F2+F3=0
From this equation, we can rearrange it to find:
F1=−(F2+F3)
Step 3: Magnitude of Forces
Since F2 and F3 are perpendicular, we can find the magnitude of their resultant using the Pythagorean theorem:
|F2+F3|=√|F2|2+|F3|2
However, since the particle is stationary, we also know:
|F1|=|F2+F3|
Step 4: Removing Force F1
Now, if we remove F1, the net force acting on the particle will be:
Fnet=F2+F3
This net force is now equal to the resultant of F2 and F3.
Step 5: Calculate the Acceleration
Using Newton's second law, the acceleration a of the particle can be calculated as:
a=Fnetm
Substituting Fnet=F2+F3:
a=F2+F3m
Since we established earlier that |F2+F3|=|F1|, we can write:
a=|F1|m
Conclusion
Thus, the acceleration of the particle after removing F1 is:
|F1|m
We have three forces acting on a particle of mass m: F1, F2, and F3. It is given that F2 and F3 are mutually perpendicular.
For the particle to remain stationary, the net force acting on it must be zero. This can be expressed mathematically as:
F1+F2+F3=0
From this equation, we can rearrange it to find:
F1=−(F2+F3)
Since F2 and F3 are perpendicular, we can find the magnitude of their resultant using the Pythagorean theorem:
|F2+F3|=√|F2|2+|F3|2
However, since the particle is stationary, we also know:
|F1|=|F2+F3|
Now, if we remove F1, the net force acting on the particle will be:
Fnet=F2+F3
This net force is now equal to the resultant of F2 and F3.
Using Newton's second law, the acceleration a of the particle can be calculated as:
a=Fnetm
Substituting Fnet=F2+F3:
a=F2+F3m
Since we established earlier that |F2+F3|=|F1|, we can write:
a=|F1|m
Thus, the acceleration of the particle after removing F1 is:
|F1|m
Topper's Solved these Questions
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - JEE Advanced ( ARCHIVE LEVEL-2)
12 Videos
- INTRODUCTION TO VECTORS & FORCES BOOK - VMC MODULES ENGLISHCHAPTER - INTRODUCTION TO VECTORS & FORCES EXERCISE - level 2
65 Videos
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Videos
- JEE MAIN - 5BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN - 5EXERCISE - PART I : PHYSICS (SECTION - 2)
5 Videos
Similar Questions
When forces F1, F2, F3, are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed then the acceleration of the particle is
View SolutionTwo forces F1 and F2 are acting on a rod abc as shown in figure.

View Solution
Knowledge Check
F1 particles are present in the mitochondria
Ain matrixBon outer membraneCon inner membraneDin intercristae space
F1 particle of oxysome
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
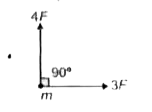
View SolutionTwo forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionLet us consider two forces F1 and F2 acting on a body of mass 2 kg as shown in the figure. F1=10N, F2=2N , what will be the acceleration?

View Solution
