A plane is inclined at an angle 30∘ with horizontal. The component of a vector →A=−10k perpendicular to this plane is: (here z-direction is vertically upwards)
5√2
5√3e
5
2.5
The correct Answer is:B
To find the component of the vector →A=−10^k that is perpendicular to a plane inclined at an angle of 30∘ with the horizontal, we can follow these steps:
1. Understand the Vector Orientation:
The vector →A=−10^k indicates that it is directed downwards along the z-axis (since ^k is the unit vector in the z-direction).
2. Identify the Plane's Orientation:
The plane is inclined at 30∘ to the horizontal. This means that the normal (perpendicular) to the plane makes an angle of 30∘ with the vertical (z-axis).
3. Determine the Normal Vector:
The normal vector to the inclined plane can be represented as:
^n=sin(30∘)^i+cos(30∘)^k
where ^i is the horizontal direction (x-axis) and ^k is the vertical direction (z-axis).
4. Calculate the Components:
- The sine and cosine values for 30∘ are:
sin(30∘)=12,cos(30∘)=√32
- Thus, the normal vector becomes:
^n=12^i+√32^k
5. Find the Component of →A Perpendicular to the Plane:
The component of the vector →A that is perpendicular to the plane can be calculated using the dot product:
Component=→A⋅^n
Substituting →A=−10^k and ^n:
Component=(−10^k)⋅(12^i+√32^k)
Since the dot product of ^i and ^k is zero, we only consider the ^k component:
Component=−10⋅√32=−5√3
6. Final Result:
The component of the vector →A that is perpendicular to the inclined plane is:
−5√3
The vector →A=−10^k indicates that it is directed downwards along the z-axis (since ^k is the unit vector in the z-direction).
The plane is inclined at 30∘ to the horizontal. This means that the normal (perpendicular) to the plane makes an angle of 30∘ with the vertical (z-axis).
The normal vector to the inclined plane can be represented as:
^n=sin(30∘)^i+cos(30∘)^k
where ^i is the horizontal direction (x-axis) and ^k is the vertical direction (z-axis).
- The sine and cosine values for 30∘ are:
sin(30∘)=12,cos(30∘)=√32
- Thus, the normal vector becomes:
^n=12^i+√32^k
The component of the vector →A that is perpendicular to the plane can be calculated using the dot product:
Component=→A⋅^n
Substituting →A=−10^k and ^n:
Component=(−10^k)⋅(12^i+√32^k)
Since the dot product of ^i and ^k is zero, we only consider the ^k component:
Component=−10⋅√32=−5√3
The component of the vector →A that is perpendicular to the inclined plane is:
−5√3
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
A particle is projected up an inclined plane with initial speed 20 m/s at an angle 30∘ with the plane. Find the component of its velocity (in m/s) perpendicular to the plane, when it strikes the plane.
View SolutionA particle is prjected up an inclined with initial speed v=20m/s at an angle θ=30∘ with the plane. The component of its velocity perpendicular to the plane when it strikes the plane is:
View SolutionA light ray is incident on a plane mirror at an angle of 30∘ with horizontal. At what angle with horizontal must a plane mirror be placed in its path so that it becomes vertically upwards after reflection?
View SolutionA force is inclined at an angle of 60∘ from the horizontal. If the horizontal component of the force is 40N. Calculate the vertical component.
View SolutionA force is inclined at an angle of 60∘ from the horizontal. If the horizontal component of the force is 4N,calculate the vertical component.
View SolutionA force is inclined at an angle of 60∘ from the horizontal. If the horizontal component of the force is 40N,calculate the vertical component.
View SolutionA body of mass 10 kg is at rest on an iinclined plane of angle 30∘ . What are its components parallel and perpendicular to the plane ?
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View Solution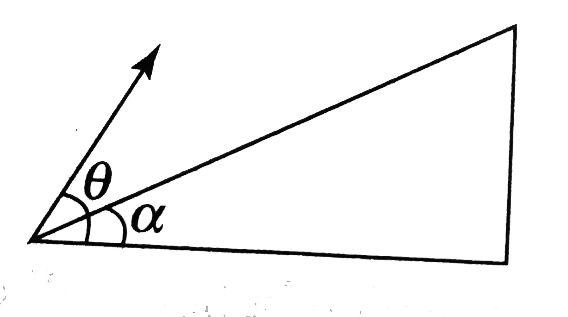
A projectile is fired at an angle θ with the horizontal. Find the condition under which it lands perpendicular on an inclined plane inclination α as shown figure.
View SolutionThe figure shows a conductor of weight 1.0N& length L=0.5m placed on a rough inclined plane making an angle 30∘ with the horizontal so that conductor is perpendicular to a uniform horizontal magnetic field of induction B=0.10T.The coefficient of static friction betwen the conductor inside the plane of is 0.1. A current of l=10A flows through the conductor inside the plane of this paper as shown.What is the force needed to be applied parallel to the inclined plane to keep the conductor at rest?

View Solution
