Two adiabatic expansions of n mole of same gas are shown. If VBVA=VDVC×12 then TC/TD is :

20.4TATB
21.4TATB
TATB12(0.4)
TATB
The correct Answer is:A
TAVγ−1A=TBVγ−1B⇒TA/TB=(VBVA)γ−1
and TCVγ−1C=TDVγ−1D⇒TC/TD=(VDVC)γ−1⇒TCTD=(2VBVA)γ−1=2γ−1TATB⇒ΔT=(165−1)1RK=115RKΔQ=ΔU+W, Here, Q : U and W all different forms of energy.For isothermal process, pV = constant ⇒ slope =dpdV=−PV
& for adiabatic process, Pvγ = constant ⇒dpdV=−γpV⇒x=γ
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 240videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )81videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - level-0 Short Answer Type – II24videos
GASEOUS STATE & THERMODYNAMICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE1videos
GRAVITATION
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionDraw the P-T and V-T diagrams for an isobabaric process of expansion, corresponding to n moles of an ideal gas at pressure P0 from V0 to 2V0
View Solution
Knowledge Check
- Question 1 - Select One
Two different adiabatic parts for the same gas intersect two isothermals at T1andT_2 as shown in P-V diagram . Then the ratio of VaVb will be
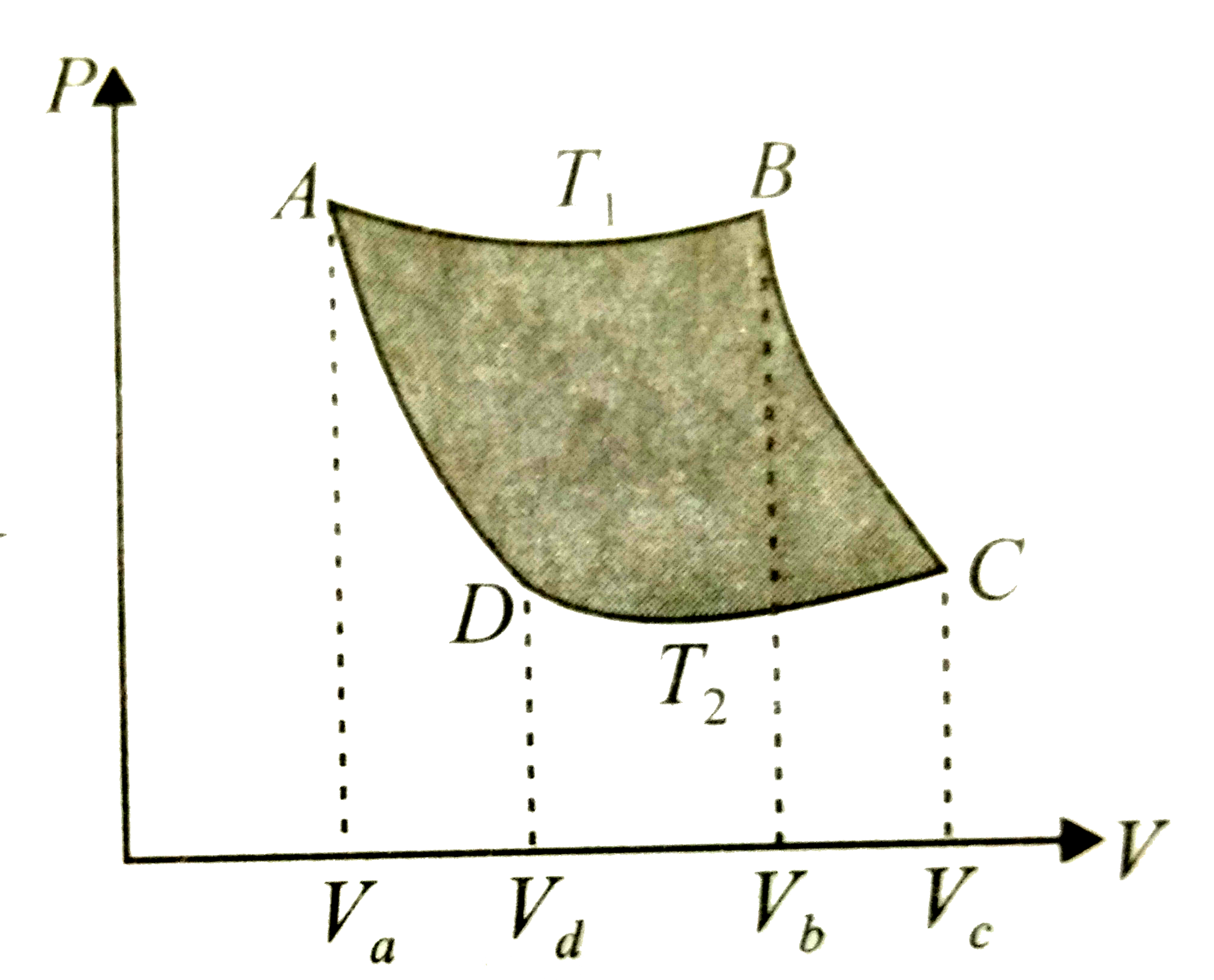 Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
Aa. VcVdBb. VdVcCc. γVdVcDd. 1γVdVc
The temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
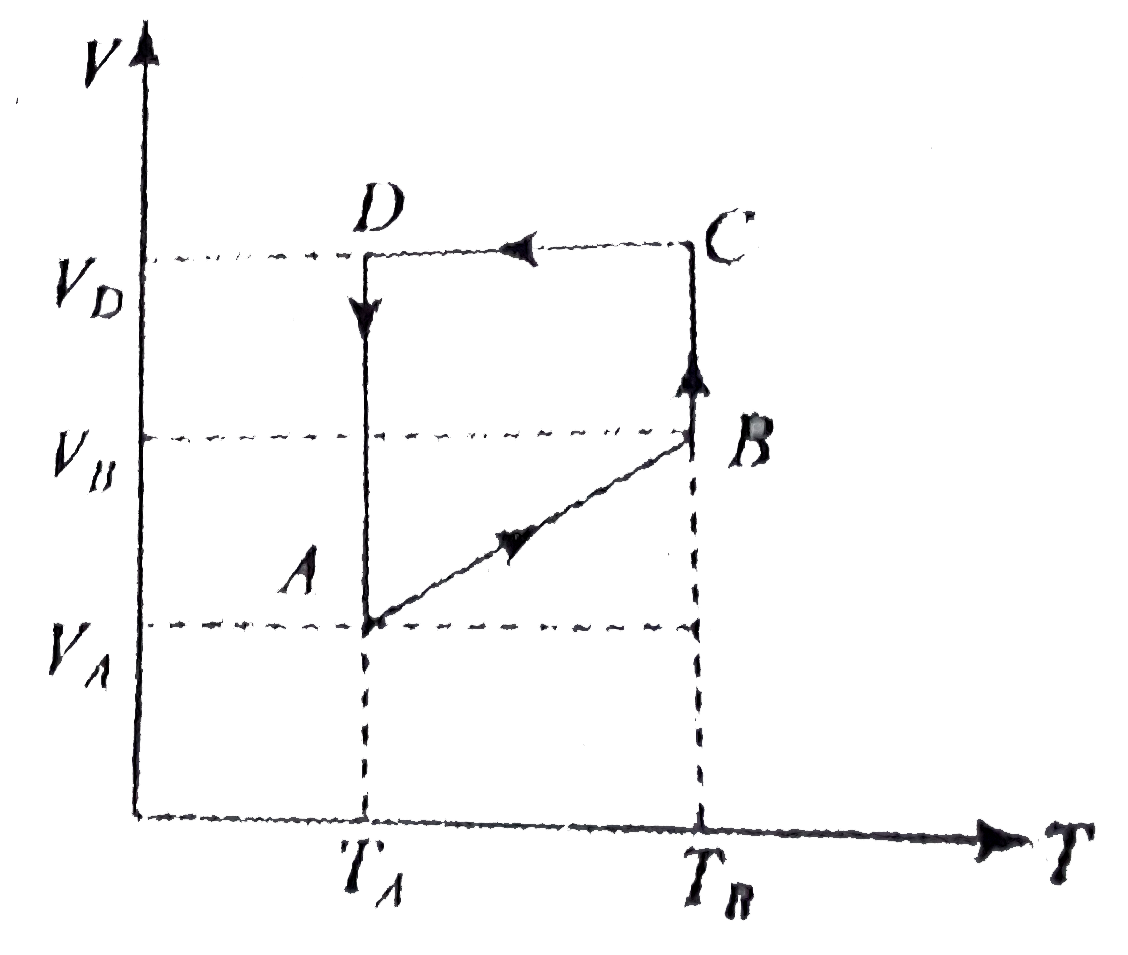
View SolutionA monotomic ideal gas of two metal is taken through a cyclic process straining from A as shown VB/VA=2andVD/VA=4 Temperature TAis27∘C
The work done during the process C→D is
 View Solution
View SolutionTwo capacitors C1 and C2 in a circuit are joined as shown. If VA=V1,VB=V2, the potential of point P is
 View Solution
View SolutionThe magnitude of ethalphy changes for reversible adiabatic expansion of a gas from volume V1 to V2(in L)is ΔH1 and for irreversible adiabatic expansion for the same expansion is ΔH2. Then
when ΔU1 and ΔU2 are the changes in magnitudes for the internal energy of gas in the two expansions.View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
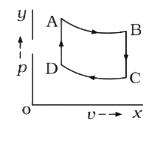
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure The pressure and temperature at A, B etc are denoted by PA,PB−,TA,TB−, etc respectively
A → B adiabatic expansion
B → C cooling at constant volume
C→D adiabatic compression
D→A heating at constant volume
Given that : TA=1000 K, PB=23PA and PC=13PA
_E01_271_Q01.png)
the heat lost by the gas in process B→CView Solution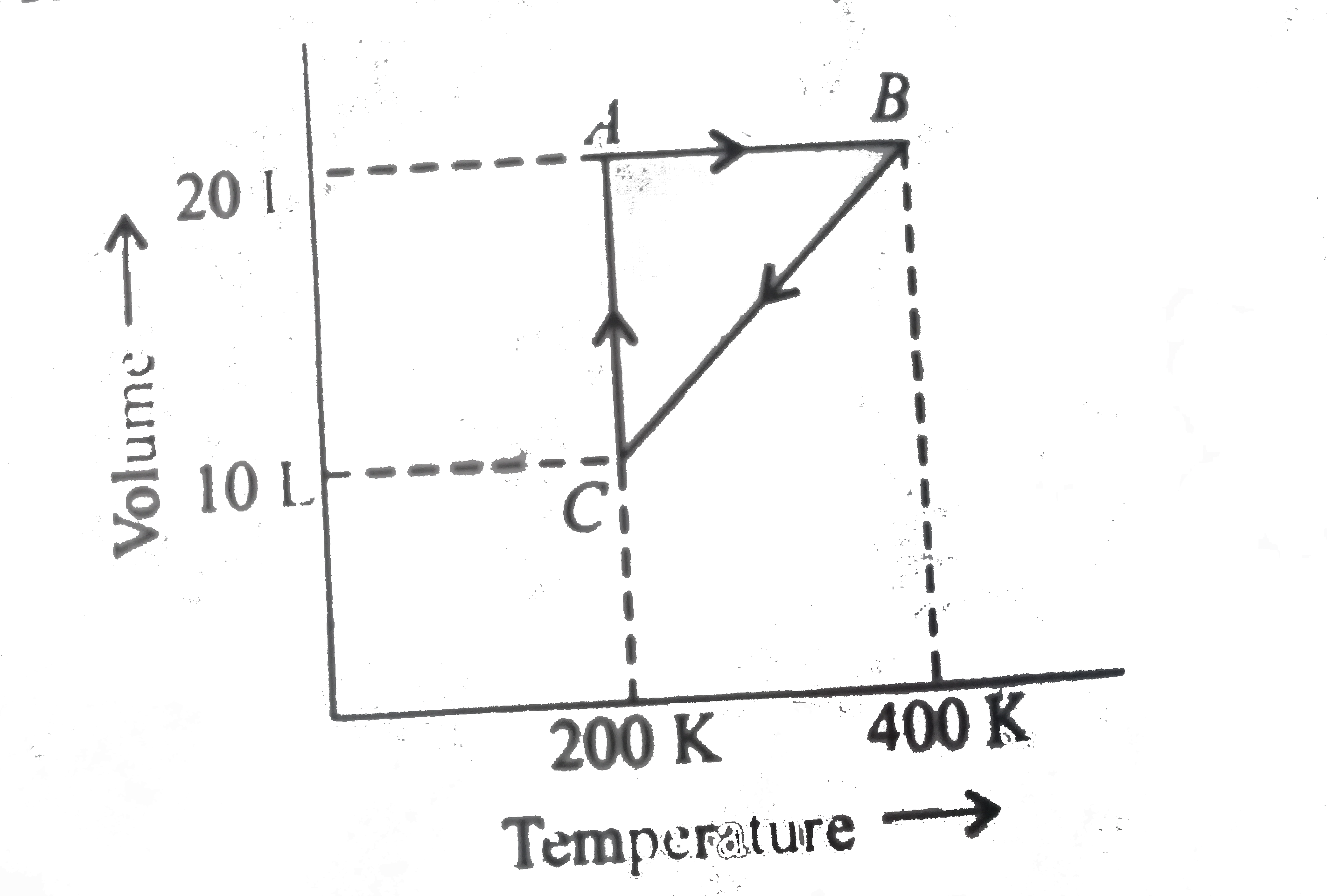
The pressure at C isView Solution

