Two radio stations broadcast their programmes at the same amplitude A and at slightly different frequencies ω1 and ω2 respectively, where ω1−ω2=103Hz. A detector receives the signals from the two stations simultaneously, it can only detect signals of intensity ≥2A2.
(i) Find the time interval between successive maxima of the intensity of the signal received by the detector.
(ii) Find the time for which the detector remains idle in each cycle of the intensity of the signal.
The correct Answer is:(i) 10−3sec,(ii)0.5×10−3sec
To solve the problem step by step, we will break it down into two parts as per the question.
Part (i): Finding the time interval between successive maxima of the intensity
1. Understanding the Signals:
We have two signals from radio stations with the same amplitude A and frequencies ω1 and ω2. The difference in frequencies is given as:
Δω=ω1−ω2=103 Hz
2. Resultant Displacement:
The resultant displacement y due to the two signals can be expressed using the principle of superposition:
y=Asin(ω1t)+Asin(ω2t)
3. Using Trigonometric Identities:
We can use the identity for the sum of sines:
y=2Acos(Δωt2)sin(ω1+ω22t)
Here, the amplitude of the resultant wave is:
A′=2Acos(Δωt2)
4. Intensity Calculation:
The intensity I is proportional to the square of the amplitude:
I∝(A′)2=(2Acos(Δωt2))2=4A2cos2(Δωt2)
5. Finding Maxima of Intensity:
For the intensity to be maximum, cos2(Δωt2) must equal 1. This occurs when:
Δωt2=nπ(n∈Z)
Thus, we can write:
t=2nπΔω
6. Time Interval Between Successive Maxima:
The time interval between successive maxima (for n and n+1):
Δt=2(n+1)πΔω−2nπΔω=2πΔω
Substituting Δω=103 Hz:
Δt=2π103≈6.283×10−3 seconds
Part (ii): Finding the time for which the detector remains idle
1. Condition for Detection:
The detector can only detect signals when the intensity I is greater than or equal to 2A2:
4A2cos2(Δωt2)≥2A2
Simplifying, we find:
cos2(Δωt2)≥12
2. Finding the Argument:
The above condition implies:
Δωt2=π4+kπ(k∈Z)
This gives us two critical points:
t1=2(π4)Δω=π2Δω,t2=2(3π4)Δω=3π2Δω
3. Calculating Idle Time:
The time interval during which the detector is idle is:
tidle=t2−t1=3π2Δω−π2Δω=2π2Δω=πΔω
Substituting Δω=103 Hz:
tidle=π103≈3.142×10−3 seconds
Final Answers:
(i) The time interval between successive maxima of the intensity is approximately 6.283×10−3 seconds.
(ii) The time for which the detector remains idle in each cycle of the intensity is approximately 3.142×10−3 seconds.
We have two signals from radio stations with the same amplitude A and frequencies ω1 and ω2. The difference in frequencies is given as:
Δω=ω1−ω2=103 Hz
The resultant displacement y due to the two signals can be expressed using the principle of superposition:
y=Asin(ω1t)+Asin(ω2t)
We can use the identity for the sum of sines:
y=2Acos(Δωt2)sin(ω1+ω22t)
Here, the amplitude of the resultant wave is:
A′=2Acos(Δωt2)
The intensity I is proportional to the square of the amplitude:
I∝(A′)2=(2Acos(Δωt2))2=4A2cos2(Δωt2)
For the intensity to be maximum, cos2(Δωt2) must equal 1. This occurs when:
Δωt2=nπ(n∈Z)
Thus, we can write:
t=2nπΔω
The time interval between successive maxima (for n and n+1):
Δt=2(n+1)πΔω−2nπΔω=2πΔω
Substituting Δω=103 Hz:
Δt=2π103≈6.283×10−3 seconds
The detector can only detect signals when the intensity I is greater than or equal to 2A2:
4A2cos2(Δωt2)≥2A2
Simplifying, we find:
cos2(Δωt2)≥12
The above condition implies:
Δωt2=π4+kπ(k∈Z)
This gives us two critical points:
t1=2(π4)Δω=π2Δω,t2=2(3π4)Δω=3π2Δω
The time interval during which the detector is idle is:
tidle=t2−t1=3π2Δω−π2Δω=2π2Δω=πΔω
Substituting Δω=103 Hz:
tidle=π103≈3.142×10−3 seconds
(i) The time interval between successive maxima of the intensity is approximately 6.283×10−3 seconds.
(ii) The time for which the detector remains idle in each cycle of the intensity is approximately 3.142×10−3 seconds.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (FILL IN THE BLANKS)17videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)4videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (MATRIX MATCH TYPE)3videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B10videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE54videos
WORK ENERGY AND POWER
Similar Questions
Two radio stations broadcast their programmes at the same amplitude A, and at slightly different frequencies ω1andω2 respectively , where ω2−ω1=103Hz. A detector receives the signals from the two stations simultaneously . It can emit signals only of intensity ≥2A2.
(i). Find the time intervals between successive maxima of the intensity of the signal received by the detector .
ii. Find the time for which the detector remains idle in each cycle of the intensity of the signal .View SolutionWhen two waves of almost equal frequencies n1 andn2 reach at a point simultaneously, what is the time interval between successive maxima ?
View Solution
Knowledge Check
- Question 1 - Select One
When two waves of almost equal frequencies v1 and v2 reach at a point simultaneously, the time interval between successive maxima is
Aυ1+υ2Bυ1−υ2C1υ1+υ2D1υ1−υ2
Find the amplitude of the electric field in a parallel bean of light of intensity 2.0Wm−2.
View SolutionThe planes sources of sound of frequency n1=400Hz,n2=401Hz of equal amplitude of a each, are sounded together. A detector receives waves from the two sources simultaneously. It can detect signals of amplitude with magnitude ≥ a only,
View SolutionTwo waves of frequency 500 Hz and 498 Hz are produced simultaneously. Calculate the time interval between successive maxima.
View SolutionTwo waves of frequencies 50 Hz and 45 Hz are produced simultaneously, then the time interval between successive maxima of the resulting wave is [maxima refers to the maximum intensity]
View Solution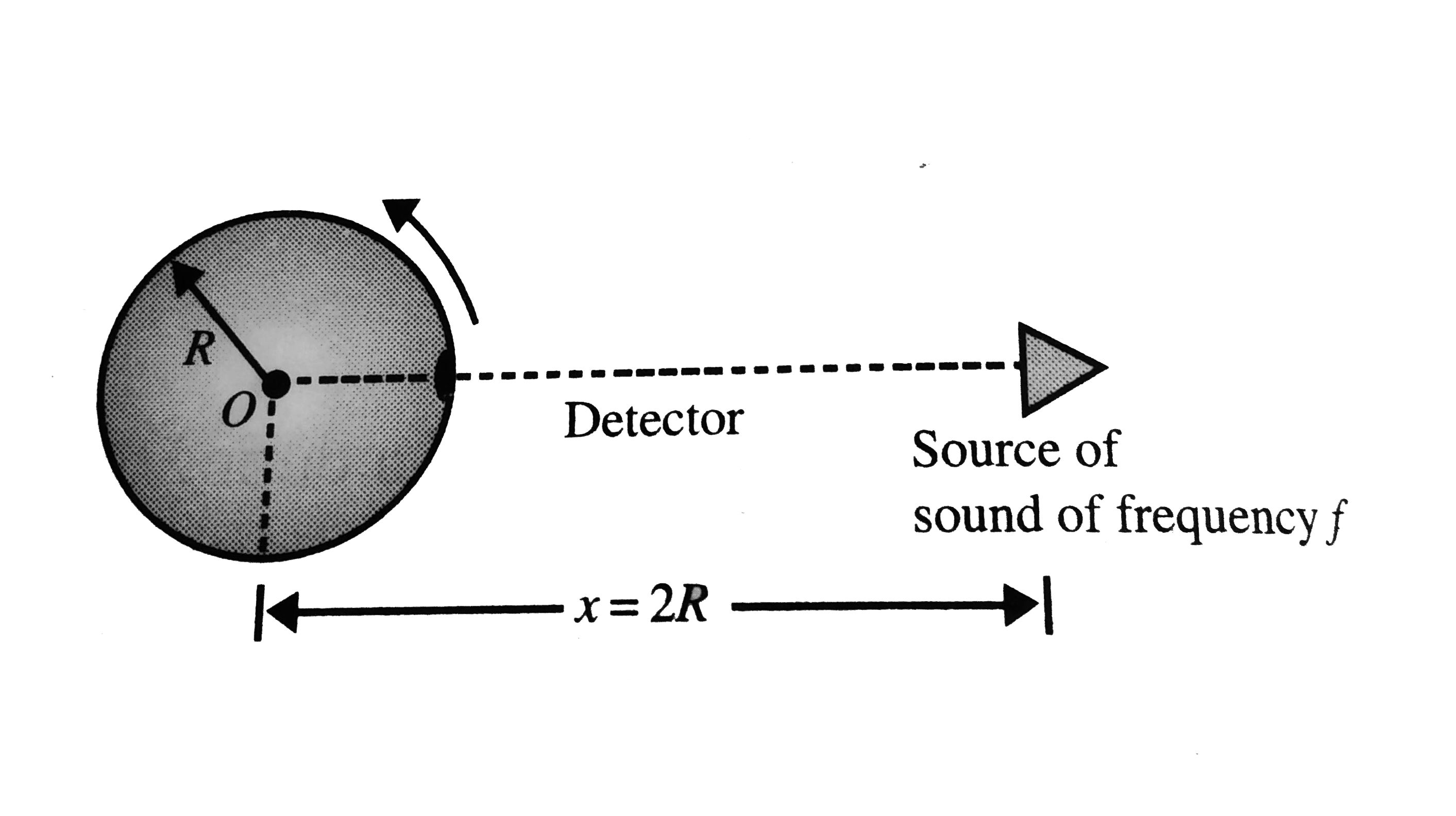
A source of sound and detector are arranged as shown in Fig. The detector is moving along a circle with constant angular speed ω. It start from the shown location in anticlockwise direction at t=0
(Take velocity of sound in air as v)
Find the time interval between minimum and maximum frequency as received by the detector.View SolutionTwo lenses have focal lengths f1 and f2 and their dispersive powers are ω1 and ω2 respectively. They will together form an achromatic combination if
View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
 View Solution
View Solution

