A thin ring of radius $R$ is made of a material of density $ρ$ and Young's modulus $Y$ . If the ring is rotated about its centre in its own plane with angular velocity $ω$ , find the small increase in its radius.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

Consider an element AB of length dl. Let T be the tension and a be the area of cross-section of the wire.

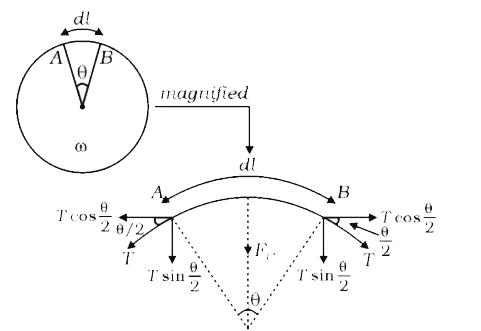
Mass of the element is dm =(Volume)(Density) $= a d l) ρ$
The component of T, i.e., $(T \frac{sin (θ)}{2} + T \frac{sin (θ)}{2})$ provides required centripetal forces to the element considered.
$∴ F_{C} = 2 T \frac{sin (θ)}{2}$
$(d m) R_{ω^{2}}^{2} = 2 T (\frac{θ}{2}) (∵ θ is small,sin \frac{θ}{2} = \frac{θ}{2})$
$T = \frac{(a d l) ρ R ω^{2}}{θ}, θ = \frac{d l}{R}$
$∴ T = a R^{2} ρ ω^{2}$ ... (i)
Let $Δ R$ be the increase in radius of the ring
Longitudinal strain $\frac{Δ l}{l} = \frac{Δ (2 π R)}{2 π R} = \frac{Δ R}{R}$
$Y = \frac{T / a}{Δ R / R} \Rightarrow Δ R = \frac{T R}{a Y}$
From Eq . (i) , $Δ R = \frac{R}{a Y} (a R^{2} ρ ω^{2}) ∴ Δ R = \frac{ρ R^{3} ω^{2}}{Y} \Rightarrow n = 2$

|

Updated on:21/07/2023

Class 12 PHYSICS PROPERTIES OF MATTER

Topper's Solved these Questions

Similar Questions

VMC MODULES ENGLISH-PROPERTIES OF MATTER-Level -2

Home
Ask Doubt
Profile