Question

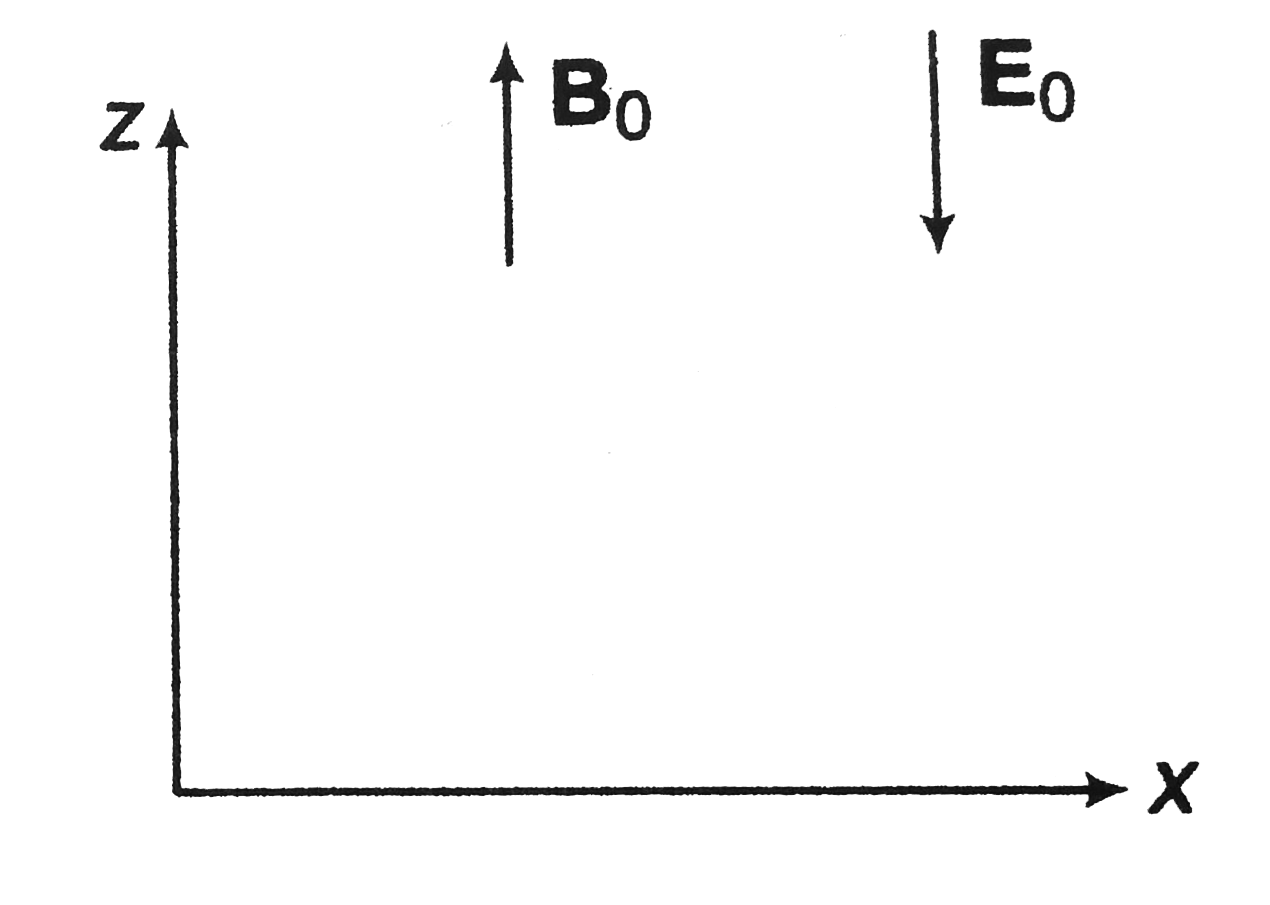
In a certain region, uniform electric field $E=-E_0\hat{k}$ and magnetic field $B=B_0\hat{k}$ are present. At time $t=0$, a particle of mass m and charge q is given a velocity $v=vj+vk$. Find the minimum speed of the particle and the time when it happens so.

Options

A. (IV) (ii) (S)
B. (II) (iii) (Q)
C. (III) (ii) (R)
D. (III) (ii) (P)

Answer

C

Explanation

For particle to move in negative y-direction, either its velocity must be in negative y-direction (if initial velocity `1= 0`) and force should be parallel to velocity or it must experience a net force in negative y-direction only (if initial velocity = 0)