IF ∣∣→A∣∣=2 and ∣∣→B∣∣=4, then match the relation in Column I with the angle θ between A and B in Column II.

Now, mark the correct above choice from the given codes :
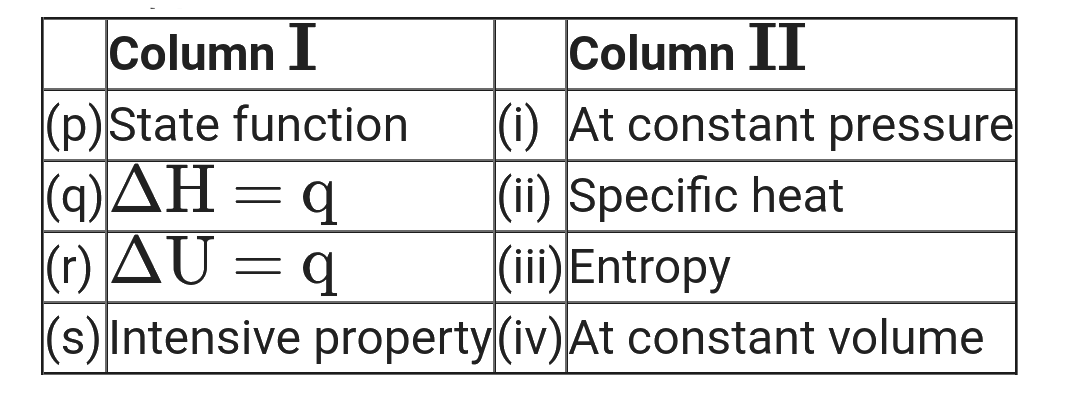
(a)p-ii, q-i, r-iv,s-iii
(b)p-iv, q-iii,r-i,s-ii
(c)p-I,q-iii,e-iv,s-ii
(d)p-iii, q-iv, r-i ,s-ii
The correct Answer is:A
Step by step video & image solution for IF |vec(A)| = 2 and |vec(B)| = 4, then match the relation in Column I with the angle theta between A and B in Column II. Now, mark the correct above choice from the given codes : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Enable
50 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
Similar Questions
If |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
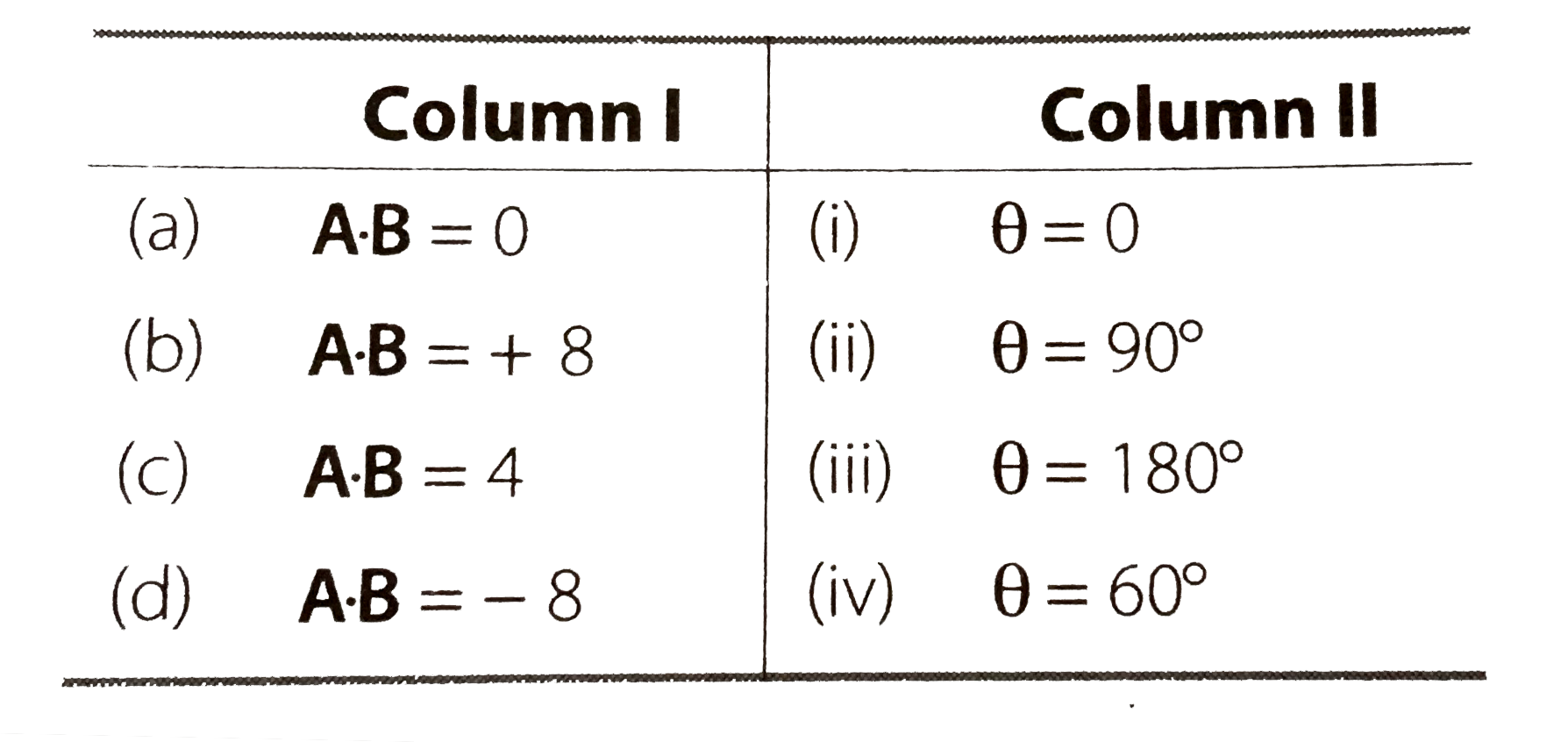
View SolutionIf ∣∣→A∣∣=2and∣∣→B∣∣=4, then match the relations in column I with the angleθ between →Aand→B in column II.
Column I, Column II
(a) ∣∣→A×→B∣∣=0 , (i) θ=30∘
(b) ∣∣→A×→B∣∣=0 , (ii) θ=45∘
(c ) →A×→B∣=4 , (iii) θ=90∘
(d) ∣∣→A×x→B∣∣=4√2 , (iv) θ=0∘.
View SolutionMatch the Column I with Column II and mark the correct option from the given codes.

View SolutionMatch the column I and with column II and mark the appropriate choice .
View SolutionMatch the column I with Column II and mark the appropriate choice .
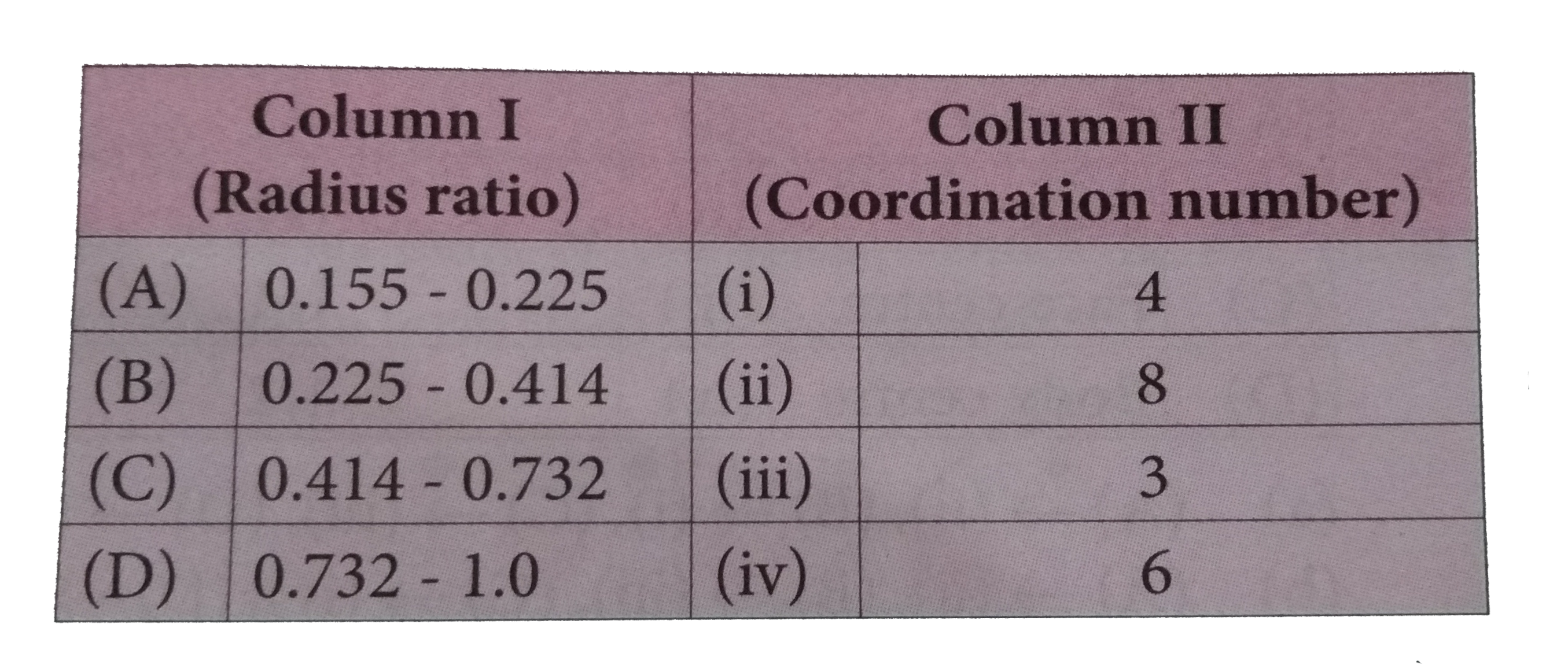
View SolutionMatch the column I with Column II and mark the appropriate choice .

View SolutionMatch the column I with Column II and mark the appropriate choice

View SolutionMatch the column I with Column II and mark the appropriate choice .
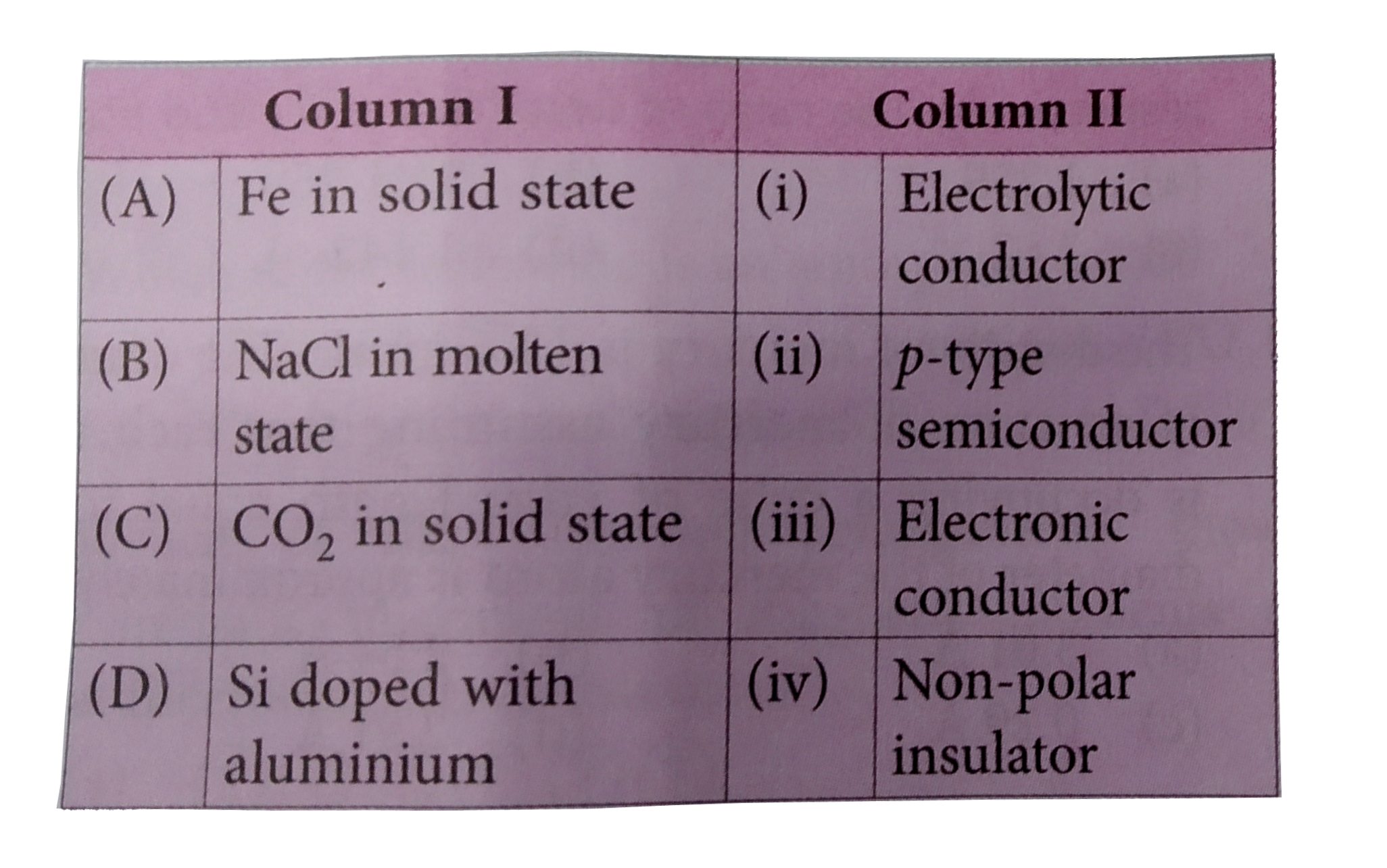
View SolutionMatch the column I with Column II and mark the appropriate choice .

View SolutionMatch the column I with Column II and mark the appropriate choice.
View Solution
