If a body is in equiliburium under a set of non-collinear forces, then the minimum number of forces has to be
Four
Three
Two
Five
The correct Answer is:B
Step by step video & image solution for If a body is in equiliburium under a set of non-collinear forces, then the minimum number of forces has to be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Enable
50 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
Similar Questions
Knowledge Check
When a body vibrates under a periodic force, the vibrations of the body are :
Anatural vibrationsBdamped vibrationsCforced vibrationsDresonant vibrations.
For a body to be in equilibrium under the combined action of several forces
View SolutionA body is in equilibrium under the influence of a number of forces. Each has a different line of action. The minimum number of forces required is.
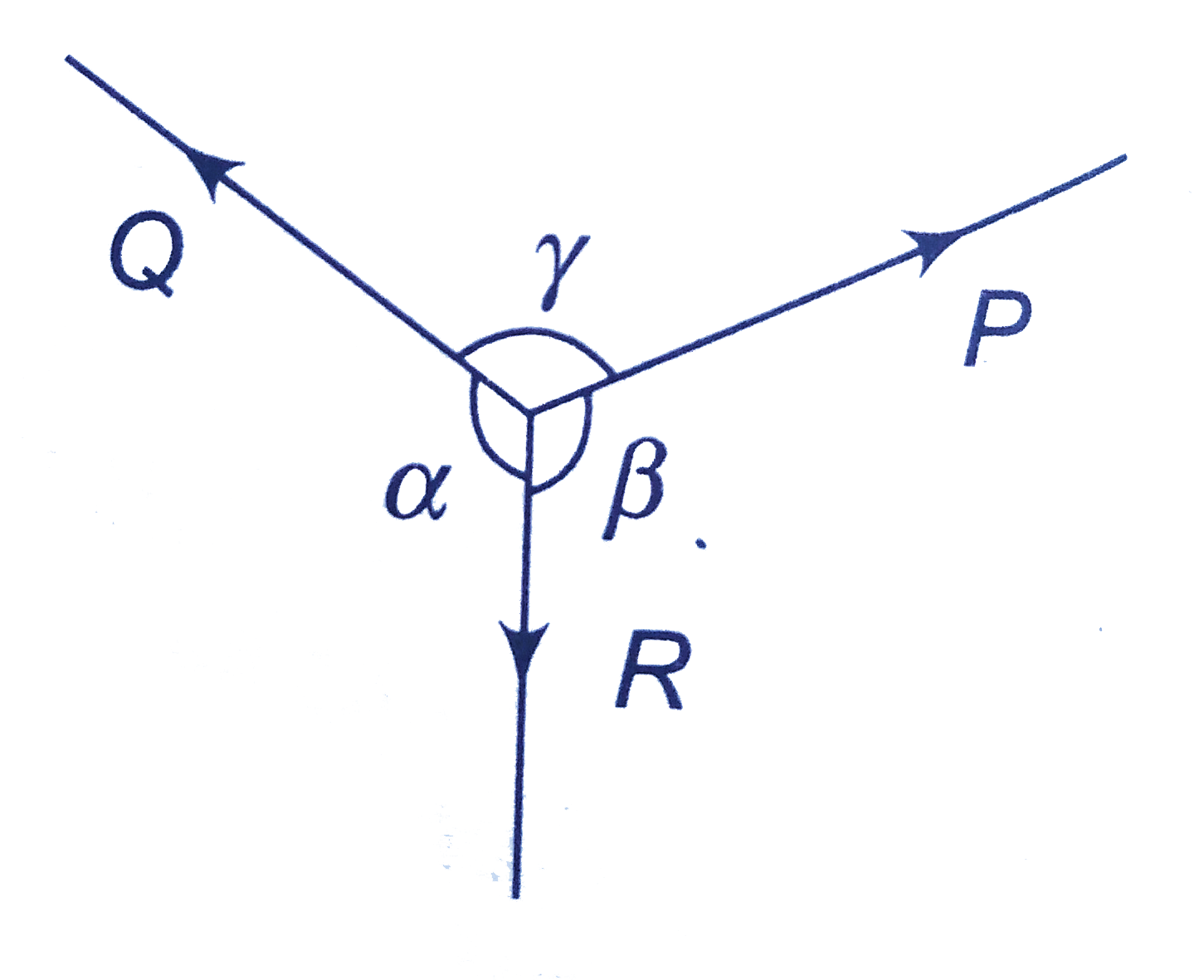
View SolutionA body is in equilibrium under the action of three coplanar forces P,QandR as shown in figure. Select the correct statement.
View SolutionHow is force related to the momentum of a body?
View SolutionThe minimum number of non coplanar forces that can keep a particle in equilibrium is
View SolutionA body has a time of 3 s under the action of one force and 4 s under the action of another force. Calculate the time period when both the forces act in the same direction simultaneously. Assume that the body undergoes the same displacement, under the action of the two different forces.
View SolutionThe vector sum of a system of non-collinear forces acting on a rigid body is given to be non-zero. If the vector sum of all torques due to the system of forces about a certain point is found to be zero, does this mean that it is necessarily zero about any arbitrary point ?
View Solution
