Let A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
:√2−1:√3−√2
1:√2:√3
1:2:3
1:4:9
The correct Answer is:A
To solve the problem, we need to determine the times of descent through segments AB, BC, and CD when a body is released from point A. Given that AB = BC = CD, we can denote the height of each segment as h.
1. Identify the heights:
Let the height of each segment (AB, BC, CD) be h. Therefore, the total height from A to D is 3h.
2. Calculate time of descent through AB:
When the body is released from A, it falls through the height h (segment AB). Using the equation of motion:
h=12gt21
Rearranging gives:
t1=√2hg
3. Calculate time of descent through BC:
The body falls through the height of 2h (from A to C). The time taken for this descent is:
2h=12gt22
Rearranging gives:
t2=√4hg=2√hg
4. Calculate time of descent through CD:
The body falls through the height of 3h (from A to D). The time taken for this descent is:
3h=12gt23
Rearranging gives:
t3=√6hg=√6hg
5. Express the times in terms of t1:
From our earlier calculations:
- t1=√2hg
- t2=2√hg=2⋅t1√2
- t3=√6hg=√3⋅t1√2
6. Find the ratio of times:
The ratio of times t1:t2:t3 can be expressed as:
t1:t2:t3=1:2:√3
Final Answer:
The times of descent through AB, BC, and CD are in the ratio 1:2:√3.
Let the height of each segment (AB, BC, CD) be h. Therefore, the total height from A to D is 3h.
When the body is released from A, it falls through the height h (segment AB). Using the equation of motion:
h=12gt21
Rearranging gives:
t1=√2hg
The body falls through the height of 2h (from A to C). The time taken for this descent is:
2h=12gt22
Rearranging gives:
t2=√4hg=2√hg
The body falls through the height of 3h (from A to D). The time taken for this descent is:
3h=12gt23
Rearranging gives:
t3=√6hg=√6hg
From our earlier calculations:
- t1=√2hg
- t2=2√hg=2⋅t1√2
- t3=√6hg=√3⋅t1√2
The ratio of times t1:t2:t3 can be expressed as:
t1:t2:t3=1:2:√3
The times of descent through AB, BC, and CD are in the ratio 1:2:√3.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - ENABLE
50 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
Knowledge Check
A, B,C and D are points on a line such that point B biscets line AC and point A bisects line CD. What is the ratio of AB to CD ?
A1/4B1/3C1/2D2/3
Let A, B and C be points in a vertical line at height h, 4h5andh5 and from the ground. A particle released from rest from the point A reaches the ground in time T. The time taken by the particle to go from B to C is TBC . Then T(TBC)2=
View SolutionIf AB =12cm, BC=16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
View SolutionLet ABC be a triangle and DandE be two points on side AB such that AD=BE. If DP∣∣BC and EQ∣∣AC, Then prove that PQ∣∣AB.
View SolutionA body is falling freely from a point A at certain height from the ground and passes through point B, C and D (vertically as shown) so that BC=CD. The time taken by the particle to move from B to C is 2 seconds and from C to D 1 second. Time taken to move from A to B in second is
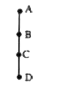
View SolutionGiven a line ABCD in which AB = BC = CD, B = (0, 3) and C = (1, 8). Find the co-ordinates of A and D.
View SolutionIn the given figure, AC is perpendicular to line PQ and BC = CD. Show that AE is greater than AB.
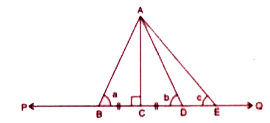
View SolutionLet A, B, C respresent the vertices of a triangle, where A is the origin and B and C have position b and c respectively. Points M, N and P are taken on sides AB, BC and CA respectively, such that (AM)/(AB)=(BN)/(BC)=(CP)/(CA)=alpha Q. AN+BP+CM is
View Solution