An elastic ball of mass m falls from a height h on an Aluminium disc of area A floating in a mercury pool. If the collision is perfectly elastic, the momentum transferred to the disc is :
√2mgh
2√mgh
m√2gh
2m√2gh
The correct Answer is:D
To solve the problem of finding the momentum transferred to the disc when an elastic ball of mass m falls from a height h and collides with it, we will follow these steps:
Step 1: Calculate the velocity of the ball just before the collision
Using the third equation of motion, we can find the velocity of the ball just before it hits the disc. The equation is given by:
v2=u2+2gh
where:
- v is the final velocity just before impact,
- u is the initial velocity (which is 0, since it starts from rest),
- g is the acceleration due to gravity,
- h is the height from which the ball falls.
Since u=0, the equation simplifies to:
v2=2gh⟹v=√2gh
Step 2: Determine the velocity after the collision
Since the collision is perfectly elastic, the velocity of the ball after the collision (v0) can be determined using the principle of conservation of momentum and the fact that the relative velocity of separation is equal to the relative velocity of approach. For a perfectly elastic collision, we have:
v0−00−v=1
This implies:
v0=−v
Substituting v:
v0=−√2gh
Step 3: Calculate the change in momentum of the ball
The change in momentum (Δp) of the ball can be calculated as follows:
Δp=pfinal−pinitial=mv0−mv
Substituting the values we found:
Δp=m(−√2gh)−m(√2gh)=−m√2gh−m√2gh=−2m√2gh
Step 4: Determine the momentum transferred to the disc
The momentum transferred to the disc is equal in magnitude but opposite in direction to the change in momentum of the ball. Therefore, the momentum transferred to the disc is:
Momentum transferred to the disc=2m√2gh
Final Answer
Thus, the momentum transferred to the disc is:
2m√2gh
---
Using the third equation of motion, we can find the velocity of the ball just before it hits the disc. The equation is given by:
- v is the final velocity just before impact,
- u is the initial velocity (which is 0, since it starts from rest),
- g is the acceleration due to gravity,
- h is the height from which the ball falls.
Since the collision is perfectly elastic, the velocity of the ball after the collision (v0) can be determined using the principle of conservation of momentum and the fact that the relative velocity of separation is equal to the relative velocity of approach. For a perfectly elastic collision, we have:
The change in momentum (Δp) of the ball can be calculated as follows:
The momentum transferred to the disc is equal in magnitude but opposite in direction to the change in momentum of the ball. Therefore, the momentum transferred to the disc is:
Thus, the momentum transferred to the disc is:
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - ENABLE
50 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - EFFICIENT
50 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A ball is dropped from height 'h' as shown.The collision is perfectly inelastic. Select the correct alternative (s)
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionSTATEMENT - 1 : Two identical balls B and C lie on a horizontal smooth straight groove so that they are touching. A third identical ball A moves at a speed v along the groove. And collides with B as shown in figure. If the collisions are perfectly elastic, then after the collision, balls A and B will come to rest and ball C moves with velocity v to the right.
because

STATEMENT - 2 : In an elastic collision, linear momentum and kinetic energy are both conserved.
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View SolutionA ball of mass m moving horizontally at a speed v collides with the bob of a simple pendulum at rest. The mass of the bob is also m. If the collision is perfectly elastic and both balls sticks, the height to which the two balls rise after the collision will be given by:
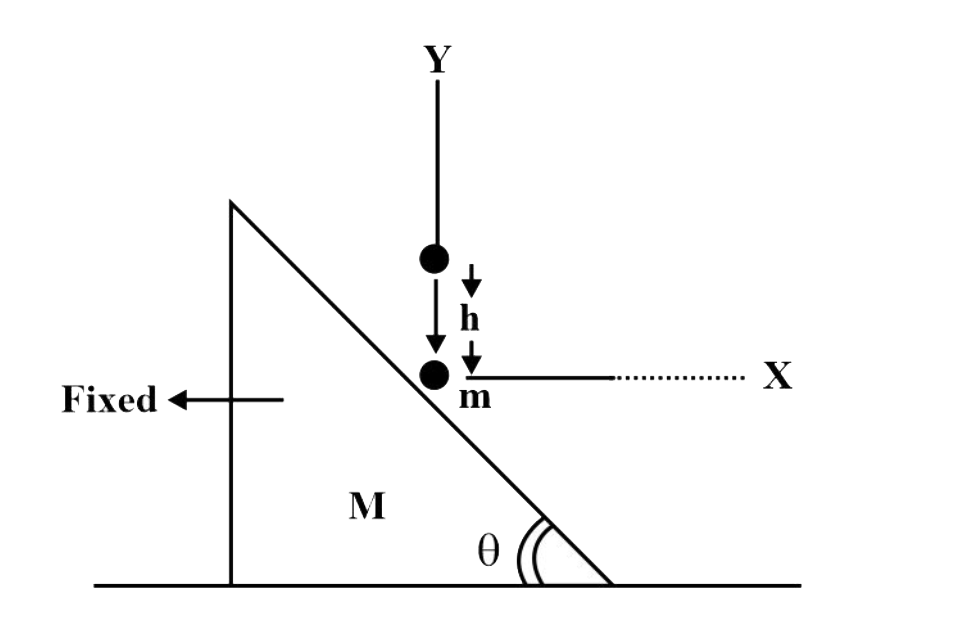
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
View SolutionA body of mass 'm' moving with certain velocity collides with another identical body at rest. If the collision is perfectly elastic and after the collision both the bodies moves
View SolutionA body of mass m falls from a height h1 and rises to a height h2. The magnitude of the change in momentum during the impact with the ground.
View SolutionA body of mass m is dropped from a height of h. Simultaneously another body of mass 2m is thrown up vertically with such a velocity v that they collide at height h2. If the collision is perfectly inelastic, the velocity of combined mass at the time of collision with the ground will be
View Solution
