Two blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
Kl040mg
Kl08mg
3Kl08mg
17Kl020mg
The correct Answer is:C
To solve the problem, we will use the work-energy theorem and the properties of springs. Here’s a step-by-step solution:
Step 1: Understand the Initial and Final Conditions
Initially, the two blocks of mass m are touching each other, and the spring is at its natural length l0. When the system is released, the spring extends by l04.
Step 2: Calculate the Total Extension of the Spring
The total extension in the spring when the blocks come to rest is given by:
Total extension=l0+l04=5l04
Step 3: Apply the Work-Energy Theorem
According to the work-energy theorem, the work done by friction is equal to the change in potential energy of the spring.
- Work done by friction:
Wfriction=−μmg(5l04)
- Potential energy of the spring:
The initial potential energy of the spring when compressed is:
PEinitial=−12kl20
The potential energy when extended is:
PEfinal=12k(l04)2=12kl2016=kl2032
Step 4: Set Up the Equation
Using the work-energy theorem:
−μmg(5l04)=(−12kl20+kl2032)
Step 5: Simplify the Right Side
Combine the potential energies:
−12kl20+kl2032=−16kl2032+kl2032=−15kl2032
Step 6: Substitute Back into the Equation
Now we can substitute this back into our equation:
−μmg(5l04)=−15kl2032
Step 7: Solve for the Coefficient of Friction μ
Rearranging gives:
μmg(5l04)=15kl2032
μ=15kl032mg⋅45
μ=12kl040mg=3kl010mg
Final Answer
Thus, the coefficient of friction μ is:
μ=3kl010mg
---
Initially, the two blocks of mass m are touching each other, and the spring is at its natural length l0. When the system is released, the spring extends by l04.
The total extension in the spring when the blocks come to rest is given by:
Total extension=l0+l04=5l04
According to the work-energy theorem, the work done by friction is equal to the change in potential energy of the spring.
Wfriction=−μmg(5l04)
The initial potential energy of the spring when compressed is:
PEinitial=−12kl20
The potential energy when extended is:
PEfinal=12k(l04)2=12kl2016=kl2032
Using the work-energy theorem:
−μmg(5l04)=(−12kl20+kl2032)
Combine the potential energies:
−12kl20+kl2032=−16kl2032+kl2032=−15kl2032
Now we can substitute this back into our equation:
−μmg(5l04)=−15kl2032
Rearranging gives:
μmg(5l04)=15kl2032
μ=15kl032mg⋅45
μ=12kl040mg=3kl010mg
Thus, the coefficient of friction μ is:
μ=3kl010mg
Similar Questions
A wooden block of mass M resting on a rough horizontal surface is pulled with a force T at an angle q to the horizontal. If m is coefficient of kinetic friction between the block and the surface, the acceleration of the block is
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :

View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .
.
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
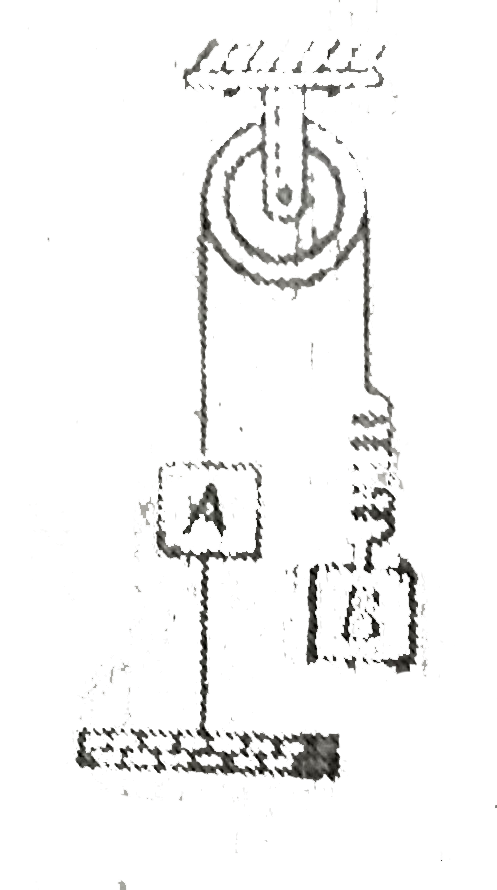
View Solution
