3 particles of mass 10 gm each are placed at the corners of an equilateral triangle of side 5 cm. The M.I. of the system about a perpendicular axis to the plane passing through a corner of the triangle will be : (in kg-m2)
5×10−2
5×10−3
5×10−4
5×10−5
The correct Answer is:D
To find the moment of inertia (M.I.) of a system of three particles located at the corners of an equilateral triangle about an axis perpendicular to the plane of the triangle and passing through one of its corners, we can follow these steps:
1. Identify the Masses and Geometry:
- Each particle has a mass m=10g=0.01kg (since we need the mass in kg).
- The side of the equilateral triangle is a=5cm=0.05m.
2. Position of the Particles:
- Let’s denote the corners of the triangle as A, B, and C.
- The axis of rotation is perpendicular to the plane of the triangle and passes through point A.
3. Calculate the Distances:
- The distance from particle A to the axis is rA=0 (since it is on the axis).
- The distance from particle B to the axis is rB=a=0.05m.
- The distance from particle C to the axis can be calculated using the height of the triangle. The height h of an equilateral triangle is given by:
h=√32a=√32×0.05m≈0.0433m
- Therefore, the distance from C to the axis is rC=h=0.0433m.
4. Moment of Inertia Calculation:
- The moment of inertia I about the axis through A is given by:
I=mAr2A+mBr2B+mCr2C
- Substituting the values:
I=0.01×02+0.01×(0.05)2+0.01×(0.0433)2
- Simplifying this:
I=0+0.01×0.0025+0.01×0.00187689
I=0.01×(0.0025+0.00187689)=0.01×0.00437689
I≈0.0000437689kg m2
5. Convert to Standard Form:
- Converting this to a more readable form:
I≈4.37689×10−5kg m2
Final Answer:
Thus, the moment of inertia of the system about the specified axis is approximately:
I≈4.38×10−5kg m2
- Each particle has a mass m=10g=0.01kg (since we need the mass in kg).
- The side of the equilateral triangle is a=5cm=0.05m.
- Let’s denote the corners of the triangle as A, B, and C.
- The axis of rotation is perpendicular to the plane of the triangle and passes through point A.
- The distance from particle A to the axis is rA=0 (since it is on the axis).
- The distance from particle B to the axis is rB=a=0.05m.
- The distance from particle C to the axis can be calculated using the height of the triangle. The height h of an equilateral triangle is given by:
h=√32a=√32×0.05m≈0.0433m
- Therefore, the distance from C to the axis is rC=h=0.0433m.
- The moment of inertia I about the axis through A is given by:
I=mAr2A+mBr2B+mCr2C
- Substituting the values:
I=0.01×02+0.01×(0.05)2+0.01×(0.0433)2
- Simplifying this:
I=0+0.01×0.0025+0.01×0.00187689
I=0.01×(0.0025+0.00187689)=0.01×0.00437689
I≈0.0000437689kg m2
- Converting this to a more readable form:
I≈4.37689×10−5kg m2
Thus, the moment of inertia of the system about the specified axis is approximately:
I≈4.38×10−5kg m2
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE50videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT50videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F10videos
SYSTEM OF A PARTICLES & ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B10videos
UNITS, MEASUREMENTS & ERRORS
Similar Questions
Three particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.View Solution
Knowledge Check
- Question 1 - Select One
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
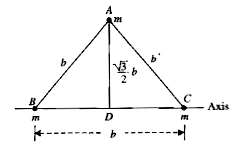 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
Three balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
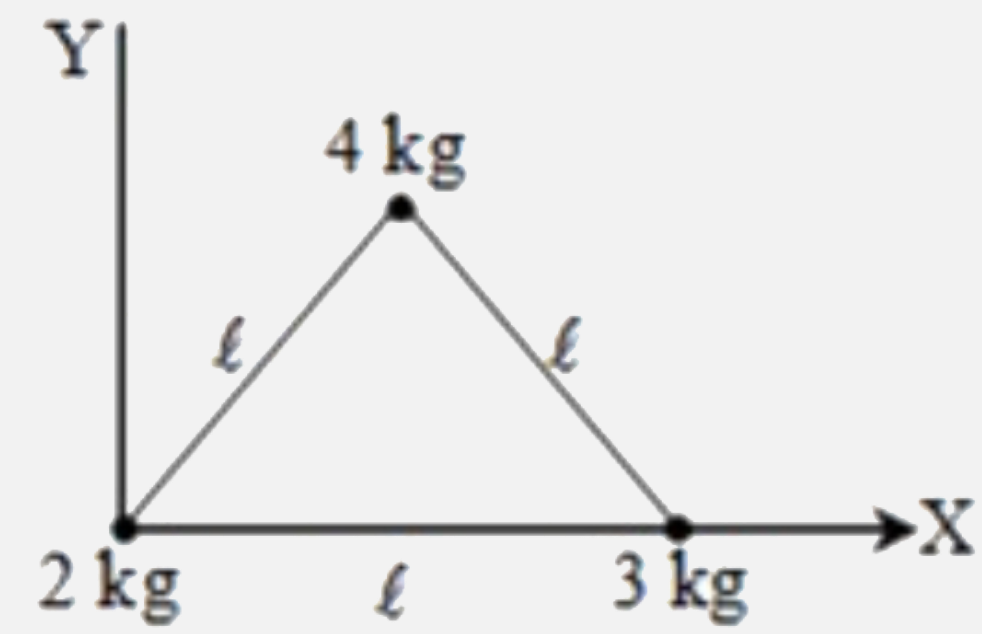
View SolutionThree masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
 View Solution
View SolutionThree particle of mas m each are placed at the three corners of an equlateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View Solution

