According to the theorem of parallel axes I=Icm+Mx2, the graph between I and x will be
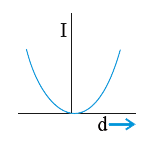
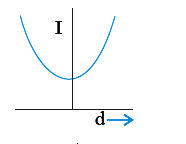

The correct Answer is:B
To solve the problem regarding the graph between moment of inertia I and distance x according to the theorem of parallel axes, we can follow these steps:
Step 1: Understand the Theorem of Parallel Axes
The theorem states that the moment of inertia I about any axis parallel to an axis through the center of mass (CM) is given by:
I=Icm+Mx2
where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass axis,
- M is the mass of the body,
- x is the distance between the two parallel axes.
Step 2: Analyze the Equation
From the equation, we can see that I is a function of x2. This indicates that the relationship between I and x is quadratic.
Step 3: Determine the Value of I at x=0
When x=0:
I=Icm+M(0)2=Icm
This means that the moment of inertia I at x=0 is equal to Icm, which is a non-zero constant.
Step 4: Behavior of I as x Increases
As x increases (either positively or negatively), the term Mx2 increases, leading to an increase in I. Thus, I increases as |x| increases.
Step 5: Graphical Representation
Since I is proportional to x2, the graph of I versus x will be a parabola opening upwards. The vertex of this parabola is at the point where x=0 and I=Icm.
Step 6: Conclusion about the Graph
The graph will not intersect the x-axis (since I is never zero for x=0), and it will be symmetric about the y-axis because I depends on x2. Therefore, the graph will extend upwards on both sides of the origin.
Final Answer
The graph between I and x will be a parabola that opens upwards, with its vertex at (0,Icm).
---
The theorem states that the moment of inertia I about any axis parallel to an axis through the center of mass (CM) is given by:
I=Icm+Mx2
where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass axis,
- M is the mass of the body,
- x is the distance between the two parallel axes.
From the equation, we can see that I is a function of x2. This indicates that the relationship between I and x is quadratic.
When x=0:
I=Icm+M(0)2=Icm
This means that the moment of inertia I at x=0 is equal to Icm, which is a non-zero constant.
As x increases (either positively or negatively), the term Mx2 increases, leading to an increase in I. Thus, I increases as |x| increases.
Since I is proportional to x2, the graph of I versus x will be a parabola opening upwards. The vertex of this parabola is at the point where x=0 and I=Icm.
The graph will not intersect the x-axis (since I is never zero for x=0), and it will be symmetric about the y-axis because I depends on x2. Therefore, the graph will extend upwards on both sides of the origin.
The graph between I and x will be a parabola that opens upwards, with its vertex at (0,Icm).
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
Knowledge Check
The intensity of a light pulse travelling along a communication channel decreases exponetially with distance x according to the relation I=I0e−ax where I0 is the intensity at x=0 and α is the attenuation constant. The percentage decrease in intensity after a distance of (In4α) is
A0.7B0.75C0.8D0.85
Statement-1: if moment of inertia of a rigid body is equal about two axis, then both the axis must be parallel.
Statement-2 from parallel axis theorem I=Icm+md2, where all terms have usual meaning.
View SolutionA,B and C are parallel conductors of equal length carrying currents I,I and 2I respectively. Distance between A and B is x. Distance between B and C is also x. F1 is the force exerted by B on A and F2 is the force exerted by B on C choose the correct answer

View SolutionAn alternating current I in an inductance coil varies with time t according to the graph as shown: Which one of the following graph gives the variation of voltage with time?
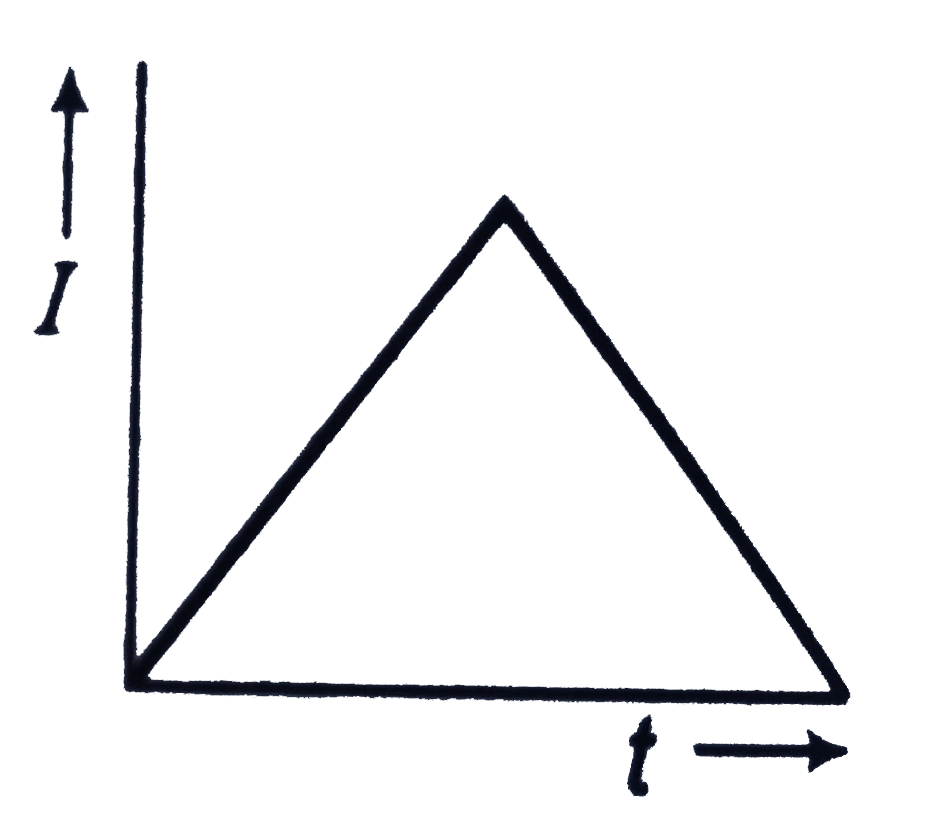
View SolutionAn alternating current I in an inductance coil varies with time t according to the graph as shown: Which one of the following graph gives the variation of voltage with time?

View SolutionUsing the scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations: 6y=5x+10,y=5x−15.
From the graph find
(i) the co-ordinates of the point where the two lines intersect,
(ii) the area of the triangle betwee the lines and the x-axis.
View SolutionAssertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
I=Icm+Mr2
View SolutionState (i) parallel axes theorem and (ii) perpendicular axes theorem.
View Solution
