In the above question, the change in angular momentum of disc in first 2 seconds in Nm second will be:
2.5
5
10
20
The correct Answer is:C
To find the change in angular momentum of the disc in the first 2 seconds, we can follow these steps:
Step 1: Identify the given values
- Moment of inertia (I) of the disc = 2 kg·m²
- Final angular velocity (ω_f) at t = 2 seconds = 5 rad/s
- Initial angular velocity (ω_i) = 0 rad/s (since the system starts from rest)
Step 2: Write the formula for angular momentum
The angular momentum (L) of a rotating object is given by the formula:
L=I⋅ω
where:
- L = angular momentum
- I = moment of inertia
- ω = angular velocity
Step 3: Calculate the final angular momentum (L_f)
Using the final angular velocity (ω_f):
Lf=I⋅ωf
Substituting the values:
Lf=2kg⋅m²⋅5rad/s=10kg⋅m²/s
Step 4: Calculate the initial angular momentum (L_i)
Using the initial angular velocity (ω_i):
Li=I⋅ωi
Substituting the values:
Li=2kg⋅m²⋅0rad/s=0kg⋅m²/s
Step 5: Calculate the change in angular momentum (ΔL)
The change in angular momentum (ΔL) is given by:
ΔL=Lf−Li
Substituting the values:
ΔL=10kg⋅m²/s−0kg⋅m²/s=10kg⋅m²/s
Step 6: Convert the units to Newton meter
Since 1 kg·m²/s is equivalent to 1 Nm, we have:
ΔL=10Nm
Final Answer
The change in angular momentum of the disc in the first 2 seconds is 10 Nm.
---
- Moment of inertia (I) of the disc = 2 kg·m²
- Final angular velocity (ω_f) at t = 2 seconds = 5 rad/s
- Initial angular velocity (ω_i) = 0 rad/s (since the system starts from rest)
The angular momentum (L) of a rotating object is given by the formula:
L=I⋅ω
where:
- L = angular momentum
- I = moment of inertia
- ω = angular velocity
Using the final angular velocity (ω_f):
Lf=I⋅ωf
Substituting the values:
Lf=2kg⋅m²⋅5rad/s=10kg⋅m²/s
Using the initial angular velocity (ω_i):
Li=I⋅ωi
Substituting the values:
Li=2kg⋅m²⋅0rad/s=0kg⋅m²/s
The change in angular momentum (ΔL) is given by:
ΔL=Lf−Li
Substituting the values:
ΔL=10kg⋅m²/s−0kg⋅m²/s=10kg⋅m²/s
Since 1 kg·m²/s is equivalent to 1 Nm, we have:
ΔL=10Nm
The change in angular momentum of the disc in the first 2 seconds is 10 Nm.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
In the above question, the angular velocity will:
View SolutionIn the above question, the value of its angular velocity after 2 seconds will be:
View SolutionIn the above question, angular displacement of the disc, in first two second will be in radian:
View SolutionThe rate of change of angular momentum is called
View SolutionA body of mass 'm' at rest is applied with a force F = (2 + 4t)N. The change in momentum of the interval one second to two second is
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
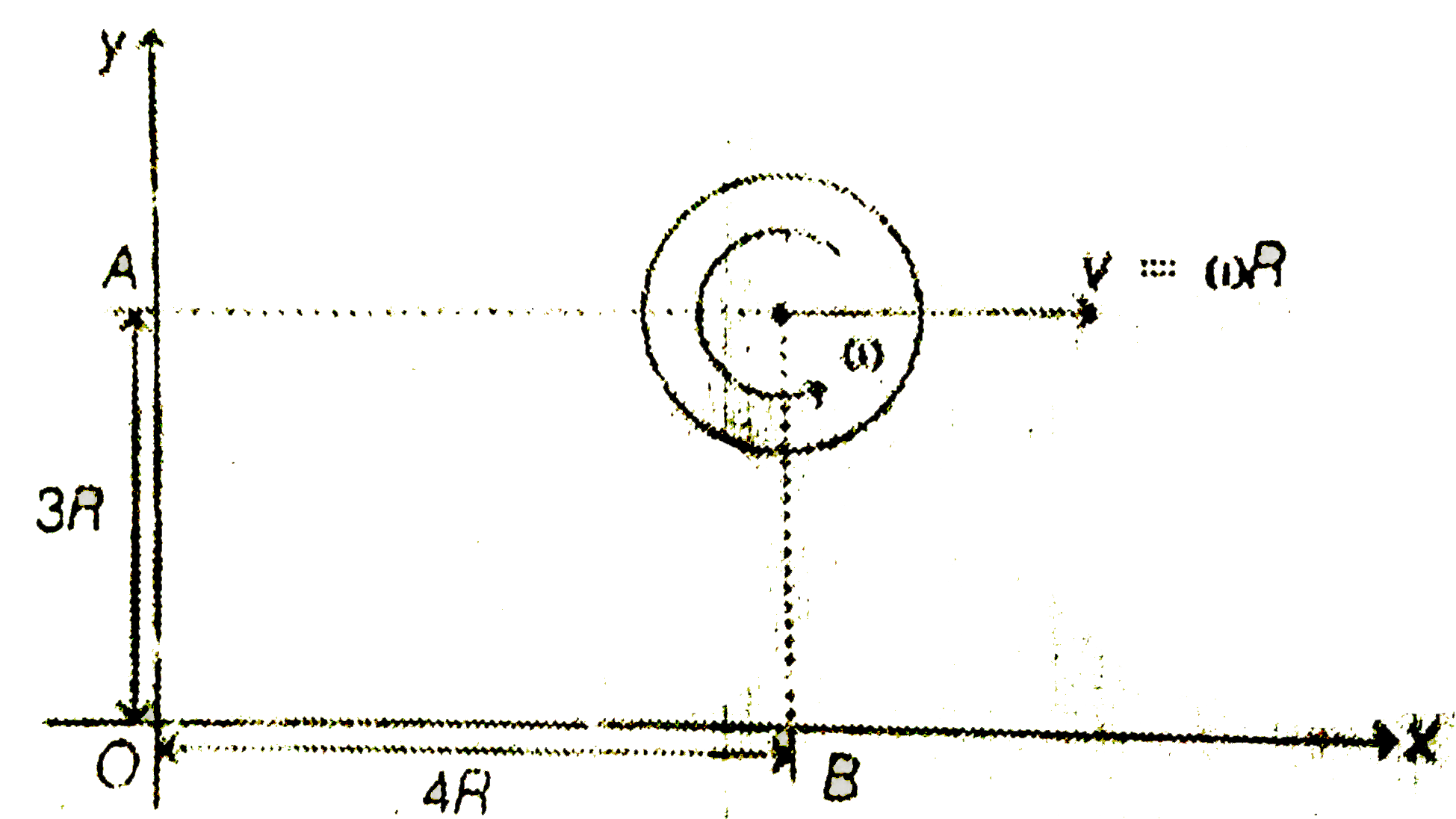
View SolutionThe angular momentum changes from 4 unit to 10 unit in 2 seconds. The torque is
View SolutionA constant torque acting on a uniform circular wheel changes its angular momentum from A0 to 4A0 in 4 seconds. Find the magnitude of this torque.
View SolutionAn orbit electron in the ground state of hydrogen has an angular momentum L1, and an orbital electron in the first orbit in the ground state of lithium (dounle ionised positively) has an angular momentum L2. Then :
View SolutionA body is freely dropped from a height h above the ground. Find the ratio of distances fallen in first one second, first two seconds, first three second first two seconds, first three seconds, also find the rato of distances fallen in 1st second, in 2nd second, in 3rd
View Solution
