Question

The curve for the moment of inertia of a sphere of constant mass M versus its radius will be:

Options

A.
B.
C.
D.

Answer

A

Explanation

To determine the curve for the moment of inertia of a sphere of constant mass $$M$$ versus its radius $$R$$, we can follow these steps:

1. Understand the Formula for Moment of Inertia:
The moment of inertia \( I \) of a solid sphere about an axis through its center is given by the formula:
\( I = \frac{2}{5} M R^2 \)
where \( M \) is the mass of the sphere and \( R \) is its radius.

2. Identify Constants:
In this case, the mass \( M \) is constant as per the problem statement. Therefore, we can treat \( \frac{2}{5} M \) as a constant term. Let’s denote this constant as \( k \):
\( k = \frac{2}{5} M \)

3. Rewrite the Moment of Inertia:
Substituting \( k \) into the equation for moment of inertia, we have:
\( I = k R^2 \)
This shows that the moment of inertia \( I \) is proportional to the square of the radius \( R \).

4. Identify the Relationship:
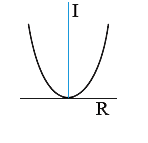
The equation \( I = k R^2 \) is in the form of a quadratic equation \( y = ax^2 \), where \( y \) represents \( I \), \( x \) represents \( R \), and \( a \) is a constant \( k \). This indicates that the graph of \( I \) versus \( R \) will be a parabola.

5. Sketch the Graph:
Since \( I \) increases with the square of the radius, the graph will be a parabola opening upwards. The x-axis will represent the radius \( R \), and the y-axis will represent the moment of inertia \( I \).

6. Conclusion:
The curve for the moment of inertia of a sphere of constant mass \( M \) versus its radius \( R \) is a parabola.