An ant is sitting at the edge of a rotating disc. If the ant reaches the other end, after moving along the diameter, the angular velocity of the disc will:-
remain constant
first decreases and then increases
first increases, then decreases
increase continuously
The correct Answer is:C
To solve the problem, we need to analyze the situation of the ant moving along the diameter of a rotating disc and how it affects the angular velocity of the disc.
1. Understand the System:
- We have a rotating disc with an ant sitting at the edge. The disc has a radius R and the ant has a mass m.
- The moment of inertia of the disc is given by Idisc=12MR2, where M is the mass of the disc.
2. Initial Moment of Inertia:
- When the ant is at the edge of the disc, the moment of inertia of the system (disc + ant) can be calculated as:
Iinitial=Idisc+mR2=12MR2+mR2
3. Conservation of Angular Momentum:
- Since there is no external torque acting on the system, angular momentum is conserved. Therefore:
Iinitial⋅ωinitial=Ifinal⋅ωfinal
- Here, ωinitial is the initial angular velocity and ωfinal is the final angular velocity after the ant moves.
4. Final Moment of Inertia:
- As the ant moves towards the center, its distance from the axis of rotation decreases. When the ant reaches the center, its contribution to the moment of inertia becomes zero.
- The final moment of inertia when the ant is at the center is:
Ifinal=Idisc+m(0)2=Idisc=12MR2
5. Analyzing the Change:
- Initially, the moment of inertia is greater than the final moment of inertia because the ant contributes mR2 when it is at the edge.
- As the ant moves from the edge to the center, the moment of inertia decreases.
6. Effect on Angular Velocity:
- From the conservation of angular momentum, since Iinitial>Ifinal, it follows that ωfinal>ωinitial.
- This means that as the ant moves towards the center, the angular velocity of the disc increases.
7. Conclusion:
- The angular velocity of the disc will initially increase as the ant moves towards the center and then will decrease after the ant crosses the center and continues to the other edge. Therefore, the correct answer is that the angular velocity of the disc will first increase and then decrease.
Final Answer:
The angular velocity of the disc will first increase and then decrease.
- We have a rotating disc with an ant sitting at the edge. The disc has a radius R and the ant has a mass m.
- The moment of inertia of the disc is given by Idisc=12MR2, where M is the mass of the disc.
- When the ant is at the edge of the disc, the moment of inertia of the system (disc + ant) can be calculated as:
Iinitial=Idisc+mR2=12MR2+mR2
- Since there is no external torque acting on the system, angular momentum is conserved. Therefore:
Iinitial⋅ωinitial=Ifinal⋅ωfinal
- Here, ωinitial is the initial angular velocity and ωfinal is the final angular velocity after the ant moves.
- As the ant moves towards the center, its distance from the axis of rotation decreases. When the ant reaches the center, its contribution to the moment of inertia becomes zero.
- The final moment of inertia when the ant is at the center is:
Ifinal=Idisc+m(0)2=Idisc=12MR2
- Initially, the moment of inertia is greater than the final moment of inertia because the ant contributes mR2 when it is at the edge.
- As the ant moves from the edge to the center, the moment of inertia decreases.
- From the conservation of angular momentum, since Iinitial>Ifinal, it follows that ωfinal>ωinitial.
- This means that as the ant moves towards the center, the angular velocity of the disc increases.
- The angular velocity of the disc will initially increase as the ant moves towards the center and then will decrease after the ant crosses the center and continues to the other edge. Therefore, the correct answer is that the angular velocity of the disc will first increase and then decrease.
The angular velocity of the disc will first increase and then decrease.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View SolutionThree ants are sitting on the vertices of an equilateral triangle of side of a... At t= 0, ant 1 starts approaching ant 2 with a speed v, ant 2 starts approaching ant 3. with a speed v and ant 3 start approaching ant 1 with a speed v. The three ant meet at the centroid of the triangle at t = 2a/3v.
Q The angular velocity of ant 2 with respect to ant 1 at t=0 is
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionA man of mass m stands on a horizontal platform in the shape of a disc of mass m and radius R, pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius r with a velocity v relative to the disc. Calculate the angular velocity of the disc.

View SolutionA thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
View SolutionA disc is rotating with angular speed ω1. The combined moment of inertia of the disc and its axle is I1. A second disc of moment of inertia I2 is dropped on to the first and ends up rotating with it. Find the angular velocity of the combination if the original angular velocity of the upper disc was (a) zero (b) ω2 in the same direction as ω1 and (c) ω2 in a direction opposite to ω1.
View Solution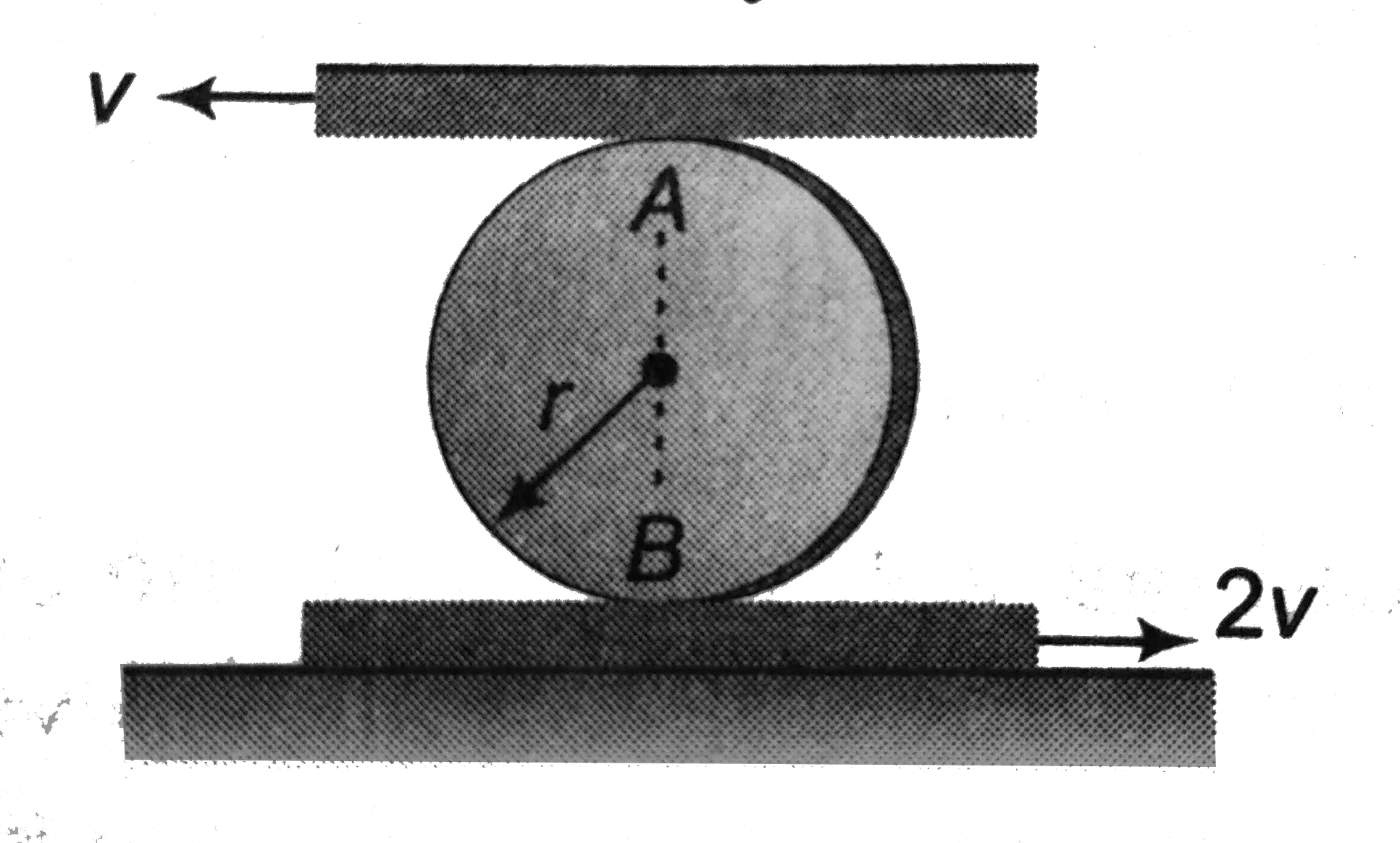
the disc of the radius r is confined to roll without slipping at A and B if the plates have the velocities shown, determine the angular velocity of the disc.
View SolutionIf a person standing on a rotating disc stretches out his hands, the angular speed will
View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionA heavy circular disc is revolving in a horizontal plane about the centre which is fixed. An insect of mass 1nth that of the disc walks from the centre along a radius and then flies away. Show that the final angular velocity is nn+2 times the original angular velocity of the disc.
View Solution
