If rotational velocity of a dynamo armature is doubled, then induced e.m.f. will become
(a)half
(b)two times
(c)four times
(d)unchanged
The correct Answer is:B
To solve the problem of how the induced electromotive force (e.m.f.) changes when the rotational velocity of a dynamo armature is doubled, we can follow these steps:
1. Understand the relationship: The induced e.m.f. (E) in a dynamo is related to the rotational velocity (ω) of the armature. The relationship can be expressed as:
E∝ω
This means that the induced e.m.f. is directly proportional to the rotational velocity.
2. Initial e.m.f.: Let the initial rotational velocity be denoted as ω1 and the corresponding induced e.m.f. as E1. According to the proportionality, we can write:
E1=k⋅ω1
where k is a constant that includes other factors such as the number of turns in the coil, the magnetic field strength, and the area of the coil.
3. Doubling the rotational velocity: If the rotational velocity is doubled, we have:
ω2=2⋅ω1
4. Calculate the new e.m.f.: Using the relationship established, the new induced e.m.f. E2 can be expressed as:
E2=k⋅ω2=k⋅(2⋅ω1)=2⋅(k⋅ω1)=2⋅E1
5. Conclusion: Thus, when the rotational velocity of the dynamo armature is doubled, the induced e.m.f. becomes:
E2=2⋅E1
Final Answer:
The induced e.m.f. will become twice the initial e.m.f..
E∝ω
This means that the induced e.m.f. is directly proportional to the rotational velocity.
E1=k⋅ω1
where k is a constant that includes other factors such as the number of turns in the coil, the magnetic field strength, and the area of the coil.
ω2=2⋅ω1
E2=k⋅ω2=k⋅(2⋅ω1)=2⋅(k⋅ω1)=2⋅E1
E2=2⋅E1
The induced e.m.f. will become twice the initial e.m.f..
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - ENABLE
50 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
Similar Questions
If the angular speed of the armature of a dynamo is doubled then the amplitude of the induced e.m.f will become_______.
View SolutionTwo identical coils, one of copper and the other of iron, are rotated with the same angular velocity ω in a uniform magnetic field. In which case the induced e.m.f. is more and why?
View Solution
Knowledge Check
A conductor is moving with the velocity v in the magnetic field and induced current is I. If the velocity of conductor becomes double, the induced current will be
A0.5 IB1.5 IC2 ID2.5 I
A coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
View SolutionIN a retangle ABCD (BC = 2AB). The moment of inertia along which aixs will be minimum
View SolutionA conducting rod is rotated about one end in a plane perpendicular to a uniform magnetic field with constant angular velocity. The correct graph between the induced emf (e) across the rod and time (t) is
View SolutionThe induced e.m.f. in a coil does not depend on
View SolutionA copper rod of length l is rotated about one end perpendicular to the uniform magnetic field B with constant angular velocity ω . The induced e.m.f. between its two ends is
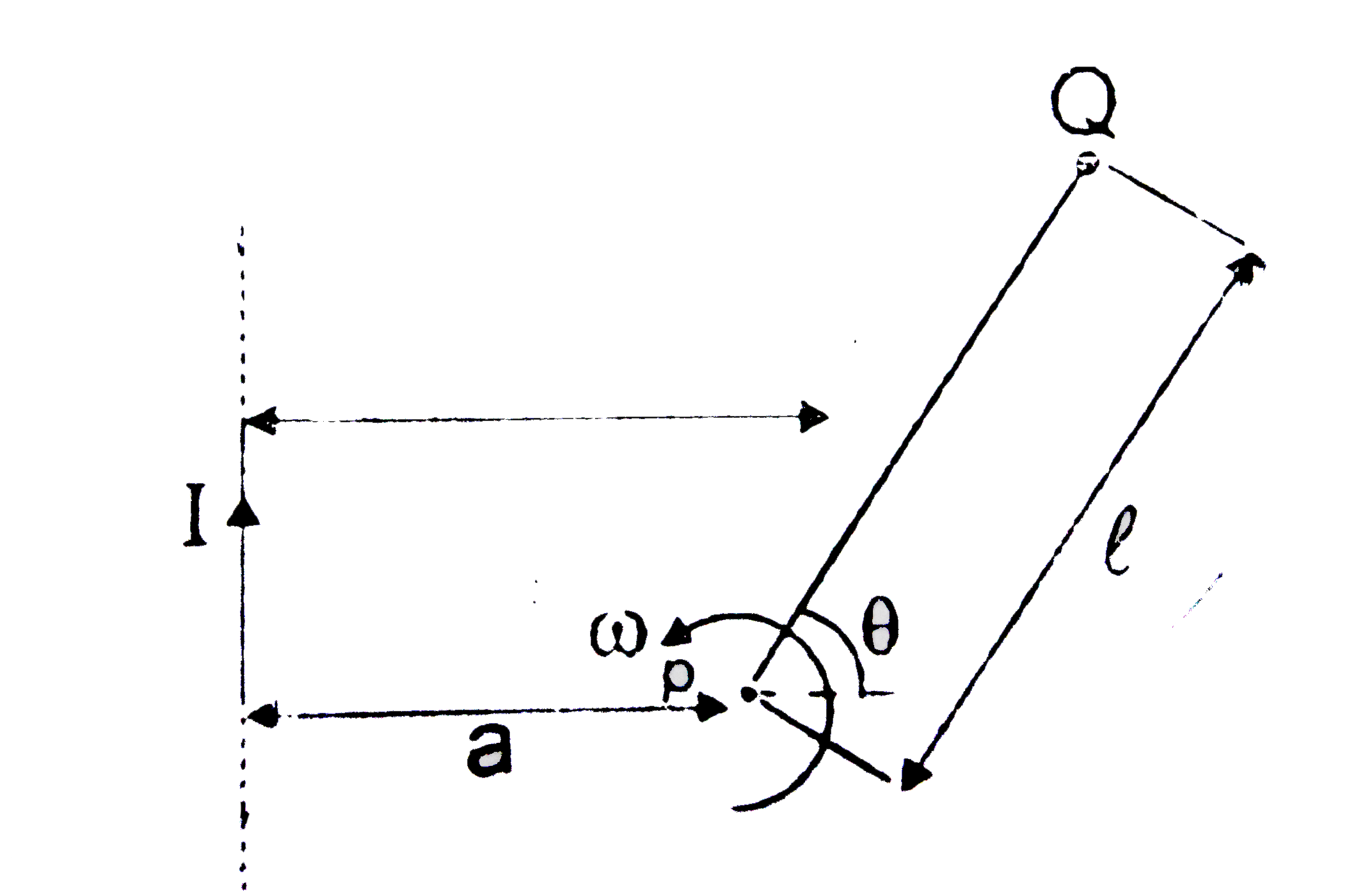
View SolutionIn the figure shown a long conductor carries constant current I. A rod PQ of length l is in the plane of the rod.The rod is rotated about point P with constant angular velocity ω as shown in the figure.Find the e.m.f induced in the rod in the position shown.Indicate which points is at high potential.
View SolutionA vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is θ. The induced e.m.f. in the rod is
View Solution
