Question

The equation $(1+2k)x+(1-k)y+k=0$, k k being parameter represents a family of lines. The line which belongs to this family and is at a maximum distance from the point (1, 4) is:

Options

A. 4x - y + 1 = 0
B. 33x + 12y 7 = 0
C. 12 x + 33y = 7
D. none of these

Answer

C

Explanation

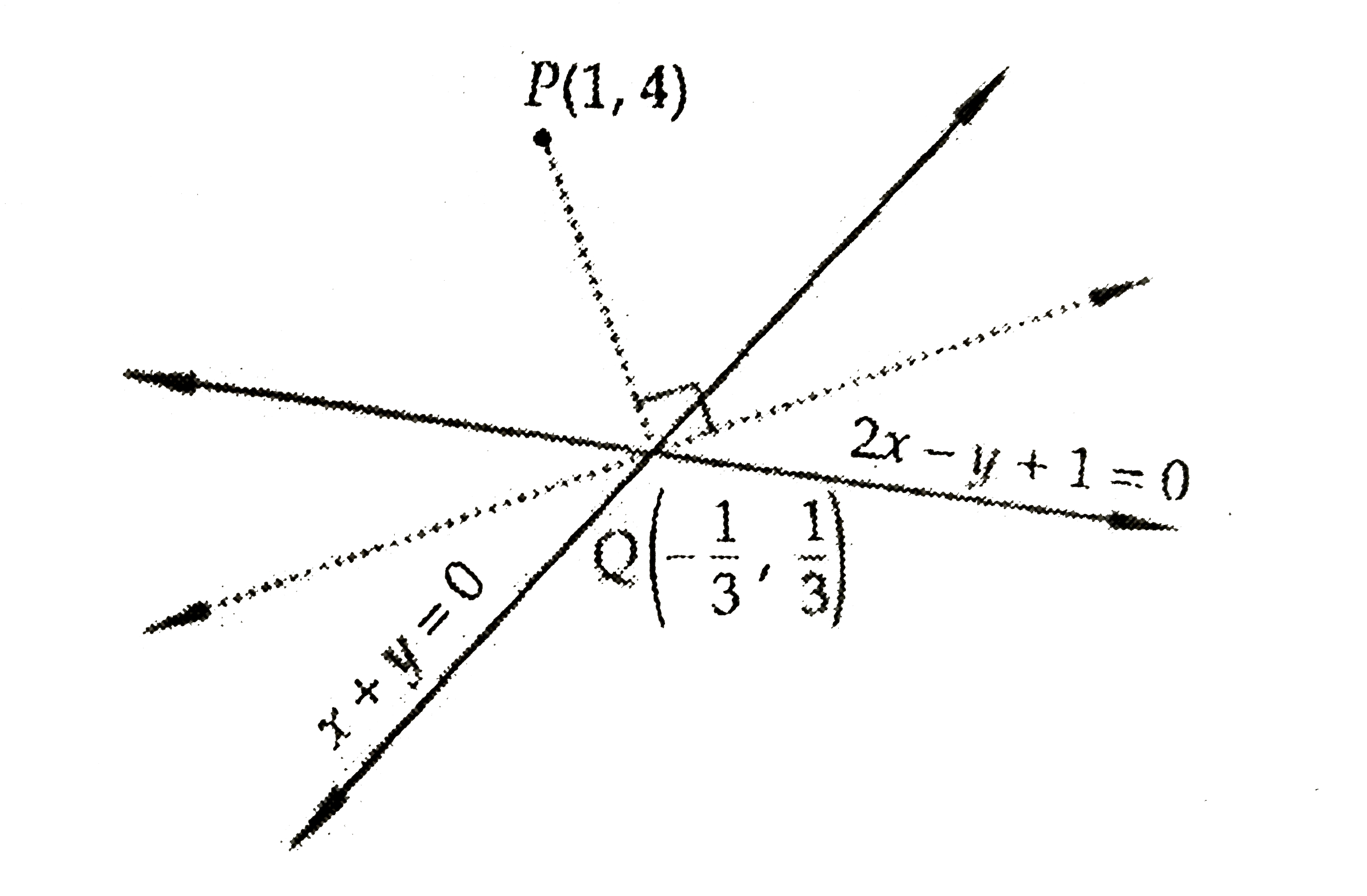
We have , x + y + `lambda (2x -y + 1) = 0`
Clearly , it represents a family of lines passing through the intersection of the lines x + y = 0 and 2x - y + 1 = 0 i.e., the point (-1/3 , 1/3).
The required the line passes through (-1/3 , 1/3) and is perpendicular to the line joining (1,4) and (-1/3 , 1/3) . So , its equation is
`y -(1)/(3) = - (4)/(11) (x + (1)/(3)) implies 12 x + 33y = 7`