△ABC is an isosceles triangle in which AB=AC, circumscribed about a circle. Prove that the base is bisccted by the point of contact.
Step by step video & image solution for triangleABC is an isosceles triangle in which AB=AC, circumscribed about a circle. Prove that the base is bisccted by the point of contact. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
7 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Revision Exercise Short Answer Questions
4 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
ABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionA triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
View Solution△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
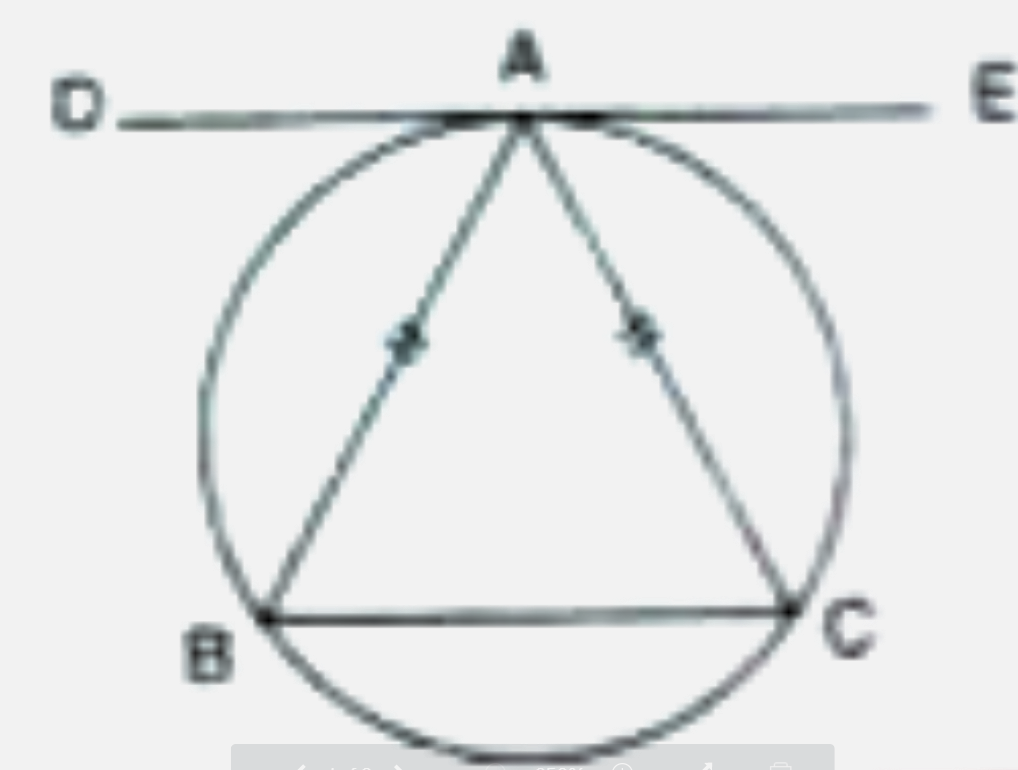
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View Solution
