Two identical billiard balls strike a rigid wall with the same speed but at different angles and get reflected without any change in speed , as shown in fig .What is (i) the diection of the force on the wall due of each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?

An instinctive answer to (i) might to be that the force on the wall in case (a) is normal to the wall , while that in case (b) is inclined at 30∘ to the normal . This answer is wrong . The force on the wall is normal to the wall in both cases . How to find the force on the wall ? the trick is to consider the force on the wall ? The trick is to consider the force ( or impulse ) on the ball due to the wall using the second law , and then use thethrid law to answer (i) .let be the speed of each ball before and after collision with the wall and m the mass of each ball .Choose the x and y axes as shown in the figure , and consider the change in momentum , of the ball in each case :
Case (a) : (Px)initial=mu (Py)intial=0
(P)initial=−mu (Py)finall=0
Impulse is the change in momentum vector .
Therefore ,
x - component of impulse = −2mu
y - component of impulse = 0
Impulse and force are in the same direction . Clearly , from above , the force on the ball due to the wall is normal to the wall along the positive x - direction . The magnitude of force cannot be ascertained since the small time taken for the collision has not been specified in the problem .
Case (b) :
(Px)initial=mucos30∘
(Py)initial=− m u sin 30∘
(Px)final=− mu cos 30∘
(Py)final =− m u sin30∘
Note , while px changes sign after collision , py does not . Therefore ,
x - component of impulse = −2 m u cos 30∘
y - component of impulse = 0
The direction of impulse (and force ) is the same as in (a) and is normal to the wall along the negative x direction . As before , using Newton.s third law , the force on the wall due to the ball is normal to the wall along the positive x direction .
The ratio of the magnitudes of the impulses imparted to the balls in (a) and (b) is
2 mu /(2mucos30∘)=2√3≈1.2
Similar Questions
Two identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionTwo identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View Solution
Knowledge Check
A rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
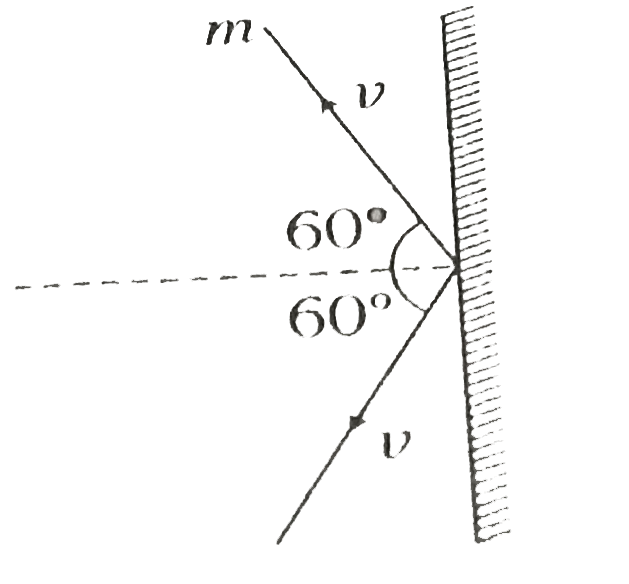 AmvB2mvCmv/2Dmv/3
AmvB2mvCmv/2Dmv/3
As shown in fig. two identical balls strike a rigid wall with equal speeds but a different angles of incidence. They are reflected back without any lose in speed.


(a) Determine the direction of force exerted by each ball on the wall.
(b) Determine the ratio of impulse imparted by the two balls on the wall in both cases.
View SolutionAs shown in fig. two identical balls strike a rigid wall with equal speeds but a different angles of incidence. They are reflected back without any lose in speed.


(a) Determine the direction of force exerted by each ball on the wall.
(b) Determine the ratio of impulse imparted by the two balls on the wall in both cases.
View SolutionA ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.
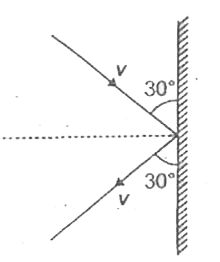
(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?
View SolutionA ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure.

(a) What is the magnitude of the impulse imparted to the ball by the wall?
(b) What is the direction of the force on the wall due to the ball?
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
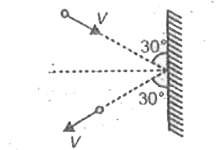
View SolutionA particle of mass m strikes a wall with speed v at an angle 30∘ with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is

View SolutionTwo billiard balls of equal mass 30 g strike a rigid wall with same speed of 108 kmph (as shown) but at different angles. If the balls get reflected with the same speed then the ratio of the magnitude of impulses imparted to ball 'a' and ball 'b' by the wall along 'X' direction is
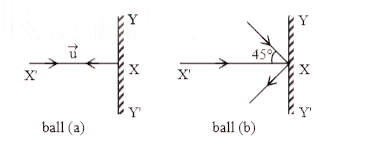
View Solution
