Two identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
To solve the problem regarding the two identical billiard balls striking a rigid wall, we will break the solution into two parts as per the question.
Part (i): Direction of the Force on the Wall
1. Understanding the Situation:
- Both billiard balls strike the wall with the same speed but at different angles.
- The first ball strikes the wall perpendicularly (90 degrees), and the second ball strikes at an angle of 30 degrees to the wall.
2. Analyzing the First Ball:
- For the first ball, which strikes perpendicularly, the change in momentum occurs entirely in the direction normal (perpendicular) to the wall.
- The force exerted on the wall due to the first ball will also be directed perpendicular to the wall.
3. Analyzing the Second Ball:
- For the second ball, which strikes at an angle of 30 degrees, we can break down the velocity into two components: one parallel to the wall and one perpendicular to the wall.
- The component of velocity perpendicular to the wall will change direction upon reflection, while the parallel component remains unchanged.
- The force exerted on the wall due to the second ball will also be directed normal to the wall, opposite to the direction of the incoming momentum.
4. Conclusion for Part (i):
- The direction of the force on the wall due to each ball is perpendicular to the wall.
Part (ii): Ratio of the Magnitudes of Impulses
1. Calculating Impulse for the First Ball:
- The impulse I1 imparted to the first ball can be calculated as:
I1=Δp=m(vf−vi)=m(−u−u)=−2mu
- The magnitude of impulse is |I1|=2mu.
2. Calculating Impulse for the Second Ball:
- For the second ball, we only consider the component of velocity that is perpendicular to the wall:
- The initial velocity component perpendicular to the wall is usin(30∘)=u2.
- The final velocity component will be −u2 (it reverses direction).
- The impulse I2 imparted to the second ball is:
I2=m(vf−vi)=m(−u2−u2)=−mu
- The magnitude of impulse is |I2|=mu.
3. Finding the Ratio of Impulses:
- Now, we can find the ratio of the magnitudes of impulses:
I1I2=2mumu=2
Final Answers:
- (i) The direction of the force on the wall due to each ball is perpendicular to the wall.
- (ii) The ratio of the magnitudes of impulses imparted to the balls by the wall is 2:1.
- Both billiard balls strike the wall with the same speed but at different angles.
- The first ball strikes the wall perpendicularly (90 degrees), and the second ball strikes at an angle of 30 degrees to the wall.
- For the first ball, which strikes perpendicularly, the change in momentum occurs entirely in the direction normal (perpendicular) to the wall.
- The force exerted on the wall due to the first ball will also be directed perpendicular to the wall.
- For the second ball, which strikes at an angle of 30 degrees, we can break down the velocity into two components: one parallel to the wall and one perpendicular to the wall.
- The component of velocity perpendicular to the wall will change direction upon reflection, while the parallel component remains unchanged.
- The force exerted on the wall due to the second ball will also be directed normal to the wall, opposite to the direction of the incoming momentum.
- The direction of the force on the wall due to each ball is perpendicular to the wall.
- The impulse I1 imparted to the first ball can be calculated as:
I1=Δp=m(vf−vi)=m(−u−u)=−2mu
- The magnitude of impulse is |I1|=2mu.
- For the second ball, we only consider the component of velocity that is perpendicular to the wall:
- The initial velocity component perpendicular to the wall is usin(30∘)=u2.
- The final velocity component will be −u2 (it reverses direction).
- The impulse I2 imparted to the second ball is:
I2=m(vf−vi)=m(−u2−u2)=−mu
- The magnitude of impulse is |I2|=mu.
- Now, we can find the ratio of the magnitudes of impulses:
I1I2=2mumu=2
- (i) The direction of the force on the wall due to each ball is perpendicular to the wall.
- (ii) The ratio of the magnitudes of impulses imparted to the balls by the wall is 2:1.
Topper's Solved these Questions
Similar Questions
Give the magnitude and direction of the net force acting on
(a) a drop of rain falling down with a constant speed
(b) a cork of mass 10 g floating on water
(c) a kite skillfully held stationary in the sky
(d) a car moving with a constant velocity of 30kh/h on a rough road
(e) a high speed electron in space free from all gravitational objects and free of electric and magnetic fields.
View SolutionEstimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3Å.
View SolutionExplain why (a) the blood pressure is humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half its value at the sea level through the 'height' of the atmospheric is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area , and force is a vector.
View SolutionAs shown in fig. two identical balls strike a rigid wall with equal speeds but a different angles of incidence. They are reflected back without any lose in speed.


(a) Determine the direction of force exerted by each ball on the wall.
(b) Determine the ratio of impulse imparted by the two balls on the wall in both cases.
View SolutionTwo identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionA rigid ball of mass m strikes a rigid wall at 60^(@) and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
View Solutionदो सर्वसम बिलियर्ड गैंडे किसी दृढ़ दीवार से समान चाल से तुरंत भिन्न कोणों पर टकराती है तथा नीच दर्शये चित्र 5.6 की भांति चाल में बिना क्षय हुए परावर्तित हो जाती है । (i) प्रत्येक गेंद के कारण दीवार पर बल की दिशा क्या है ? तथा (ii) दीवार द्वारा दोनों गेंदोंपर लगे आवेगों का अनुपात क्या है?
View Solutionदो सर्वसम बिलियर्ड गेंदें किसी दृढ़ दीवार से समान चाल से , परंतु भिन्न कोनों पर टकराती है तथा नीचे दर्शाए चित्र की भाँति चाल में बिना क्षय हुए परावर्तित हो जाती है ।
(i) प्रत्येक गेंद के कारण दीवार पर बल की दिशा क्या है ? तथा (ii) दीवार द्वारा दोनों गेंदों पर लगे आवेगों का अनुपात क्या है ?
View SolutionA ball of mass m strikes a rigid wall with speed v and gets reflected without any loss of speed, as shown in the figure. (a) What is the magnitude of the impulse imparted to the ball by the wall? (b) What is the direction of the force on the wall due to the ball?
View SolutionTwo identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any change in speed, as shown in Fig. 5.6. What is (i) the direction of the force on the wall due to each ball? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
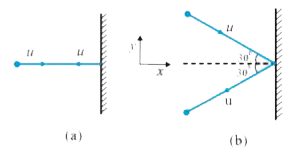
View SolutionTwo identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any change in speed, as shown in Fig. 5.6. What is (i) the direction of the force on the wall due to each ball? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
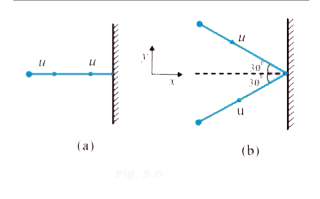
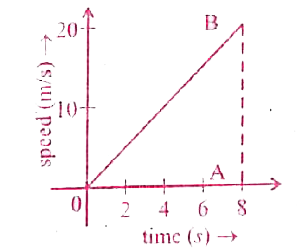
View SolutionThe speed of a car as a function of time as shown figure. Find the acceleration and distance travelled by the car in 8 seconds .
View SolutionA rigid ball of mass m strikes a rigid wall at 60° and gets reflected without loss of speed as shown in the fiugre below. The value impulse imparted by the wall on the ball will be:
View SolutionTwo identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any change in speed, as shown in figure. What is (i) the direction of the force on the wall due to each ball? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionA rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
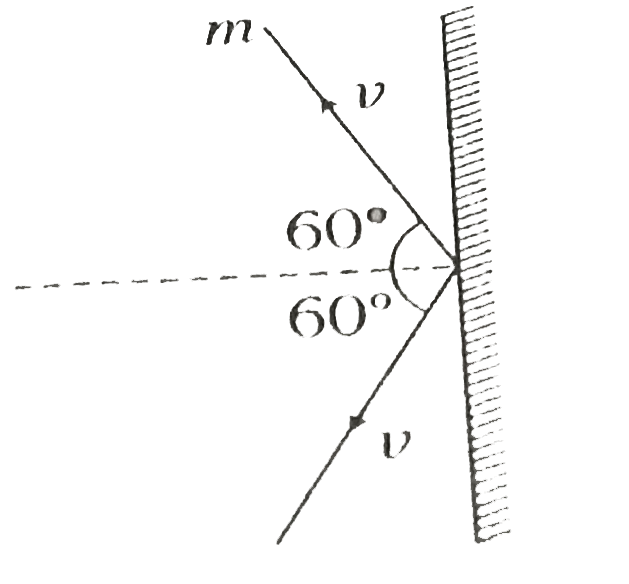
View Solution
