△ABC-এর মধ্যমা তিনটি AD, BE ও CF পরস্পর G বিন্দুতে মিলিত হয়েছে। প্রমাণ করো, △GBD=16△ABC।
Step by step video & image solution for /_\ABC-এর মধ্যমা তিনটি AD, BE ও CF পরস্পর G বিন্দুতে মিলিত হয়েছে। প্রমাণ করো, /_\GBD=1/6 /_\ABC। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ক্রয়মূল্য ও বিক্রয়মূল্যের অনুপাত 10:11 হলে, শতকরা লাভ -
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIn given figure the altitudes AD, BE and CF , the altitudes of triangle ABC are equal. Prove that ABC is an equilateral triangle.
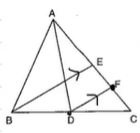
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionIn a triangle ABC,AD,BE,CF intersects each other at G, show that BE+CF>(3)/(2)BC
View SolutionAD, BE and CF asre the medians of a triangle ASBC intersectiing in G. Show that △AGB=△BGC=△CGA=13△ABC.
View SolutionConstruct a triange ABC in which AD,BE and CF are the medians with AD=5.4cm,BE=6 cm and CF=8.1cm.
View Solutionचित्र में यदि ΔFEC≅ΔGBD तथा ∠1=∠2 हो तो सिद्ध करो की ΔADE~ΔABC
View SolutionIf AD, BE and CF are the medians of a ABC ,then (AD2+BE2+CF2):(BC2+CA2+AB2) is equal to
View Solutionयदि AD, BE और CF एक त्रिभुज ABC कि मध्यिकाएँ है, तो सिद्ध करें कि −−→AD+−−→BE+−−→CF=→0
View Solution25^(@)C In warmth Br_2(g)-এর প্রমাণ গঠন-তাপ +30.9kJmol^(-1) |এই উষ্ণতায় Br_2(l) -এর বাষ্পায়নের এনথ্যালপি ( kJmol ^ (- 1) )-
View SolutionΔABC లో AD, BE , CF లు A,B C శీర్షాల నుంచి ఎదుటి భుజాలకు గీసిన లంబాలయితే 1 / AD + 1 / BE + 1 CF = 1 /r అని చూపండి.
View SolutionAD, BE and CF are altitudes of △ ABC. If AD = BE = CF, prove that △ ABC is an equilateral triangle.
View SolutionIn ΔABC, if AD , BE , CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides, shot that
1AD+1BE+1CF=1rand(ii)AD.BE.CF=(abc)28R3=8Δ3abc
View Solution
