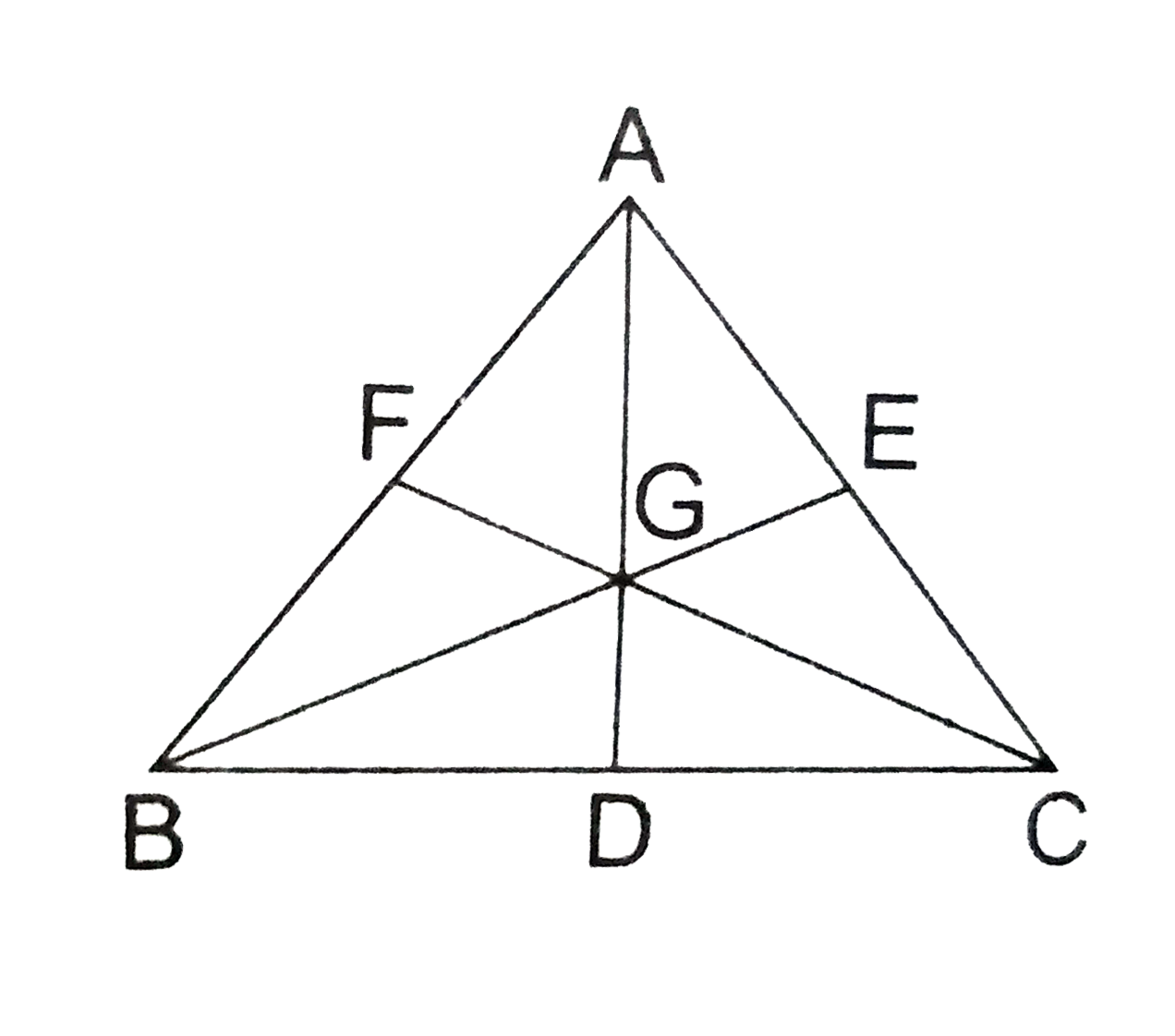
AD, BE and CF asre the medians of a triangle ASBC intersectiing in G. Show that △AGB=△BGC=△CGA=13△ABC.
Step by step video & image solution for AD, BE and CF asre the medians of a triangle ASBC intersectiing in G. Show that /_\AGB=/_\BGC=/_\CGA=1/3/_\ABC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Let BE and CF be the two medians of a△ABC and G be the intersection. Also, let EF cut AG at O, then AO : OG is
A1:1B1:2C2:1D3:1
If the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
View SolutionA(5, 4), B(-3, -2) and C(1,-8) are the vertices of a triangle ABC. Find the equation of median AD
View SolutionAD,BE and CF are the medians of a ΔABC. Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIn a triangle ABC, AD,BE,CF intersects each other at G, show that BE+CF>32BC.
View SolutionIf AD,BEandCF be the median of a △ABC, prove that −−→AD+−−→BE+−−→CF=0
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn A ΔABC,AD,BEandCF are three medians . The perimeter of ΔABC is always
View Solution
