A hollow cylinder of mass m made heavy at its bottom is floating vertically in water. It is tilted from its vertical position through an angle θ and is left. The restoring force acting on it is
mgcosθ
mgsinθ
mg[1cosθ−1]
mg[1cosθ+1]
The correct Answer is:C
To solve the problem of finding the restoring force acting on a hollow cylinder that is floating vertically in water and tilted at an angle θ, we can follow these steps:
1. Understand the System:
- We have a hollow cylinder of mass m that is made heavy at its bottom. When it is floating vertically, it is in equilibrium due to the balance of forces: the weight of the cylinder and the buoyant force (upthrust) acting on it.
2. Identify Forces:
- The weight of the cylinder is given by W=mg.
- The buoyant force (upthrust) when the cylinder is vertical can be expressed as:
Fb=Vdisplaced⋅ρ⋅g
where Vdisplaced is the volume of water displaced, ρ is the density of water, and g is the acceleration due to gravity.
3. Volume of Water Displaced:
- When the cylinder is vertical, the volume of water displaced is equal to the volume of the submerged part of the cylinder. If A is the cross-sectional area and L is the length of the cylinder, then:
Vdisplaced=A⋅L
- Thus, the buoyant force when the cylinder is vertical is:
Fb=A⋅L⋅ρ⋅g
4. Tilt the Cylinder:
- When the cylinder is tilted at an angle θ, the length of the cylinder submerged in water changes. The new submerged length can be expressed as Lcosθ.
- The new volume of water displaced becomes:
Vdisplaced=A⋅(Lcosθ)
- Therefore, the new buoyant force when tilted is:
F′b=A⋅(Lcosθ)⋅ρ⋅g
5. Calculate the Restoring Force:
- The restoring force Fr is the difference between the original buoyant force and the new buoyant force when tilted:
Fr=Fb−F′b=A⋅L⋅ρ⋅g−A⋅(Lcosθ)⋅ρ⋅g
- Simplifying this gives:
Fr=A⋅L⋅ρ⋅g(1−cosθ)
6. Express in Terms of Mass:
- Since m=A⋅L⋅ρ, we can substitute this into our equation:
Fr=m⋅g⋅(1−cosθ)
Final Answer:
The restoring force acting on the hollow cylinder when tilted at an angle θ is:
Fr=mg(1−cosθ)
- We have a hollow cylinder of mass m that is made heavy at its bottom. When it is floating vertically, it is in equilibrium due to the balance of forces: the weight of the cylinder and the buoyant force (upthrust) acting on it.
- The weight of the cylinder is given by W=mg.
- The buoyant force (upthrust) when the cylinder is vertical can be expressed as:
Fb=Vdisplaced⋅ρ⋅g
where Vdisplaced is the volume of water displaced, ρ is the density of water, and g is the acceleration due to gravity.
- When the cylinder is vertical, the volume of water displaced is equal to the volume of the submerged part of the cylinder. If A is the cross-sectional area and L is the length of the cylinder, then:
Vdisplaced=A⋅L
- Thus, the buoyant force when the cylinder is vertical is:
Fb=A⋅L⋅ρ⋅g
- When the cylinder is tilted at an angle θ, the length of the cylinder submerged in water changes. The new submerged length can be expressed as Lcosθ.
- The new volume of water displaced becomes:
Vdisplaced=A⋅(Lcosθ)
- Therefore, the new buoyant force when tilted is:
F′b=A⋅(Lcosθ)⋅ρ⋅g
- The restoring force Fr is the difference between the original buoyant force and the new buoyant force when tilted:
Fr=Fb−F′b=A⋅L⋅ρ⋅g−A⋅(Lcosθ)⋅ρ⋅g
- Simplifying this gives:
Fr=A⋅L⋅ρ⋅g(1−cosθ)
- Since m=A⋅L⋅ρ, we can substitute this into our equation:
Fr=m⋅g⋅(1−cosθ)
The restoring force acting on the hollow cylinder when tilted at an angle θ is:
Fr=mg(1−cosθ)
Similar Questions
Knowledge Check
A Body moves 6m north, 8m east and 10m vertically upwards, what is its resultant displacement from initial position
A10√2 mB10 mC10√2 mD20 m
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA cylindrical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA body is mass m is rotating in a vertical circle of radius 'r' with critical speed. The difference in its K.E at the top and at the bottom is
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
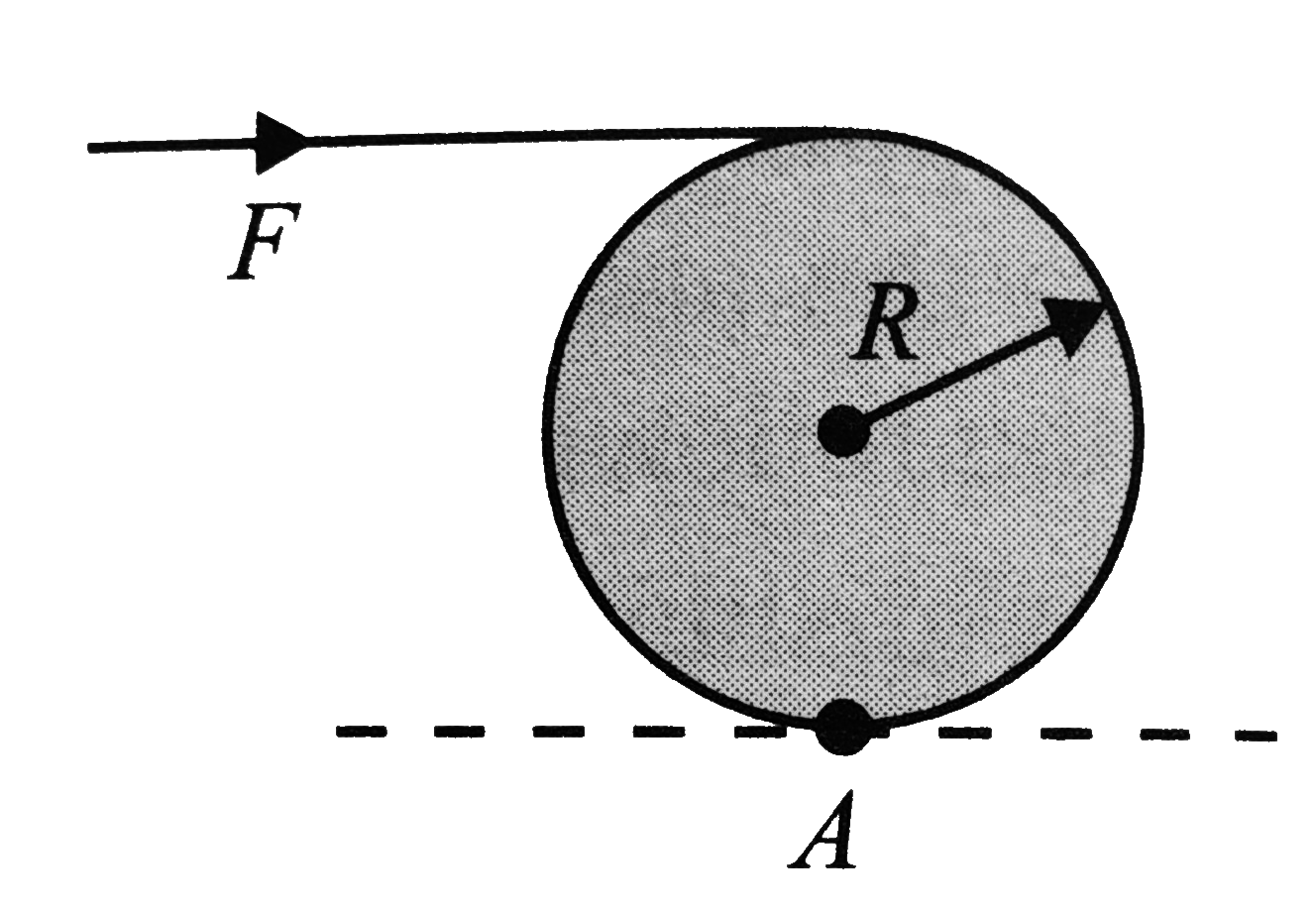
Component of reaction at the hinge in the vertical direction is
View Solution
