Two loops P and Q are made from a uniform wire. The redii of P and Q are respectively, and their moments of inertia are respectively, If-
The correct Answer is:B
To solve the problem, we need to find the ratio of the radii r2r1 given that the moment of inertia I2=4I1.
1. Understanding the Moment of Inertia for Circular Loops:
The moment of inertia I for a circular loop is given by the formula:
I=m⋅r2
where m is the mass of the loop and r is the radius.
2. Expressing Mass in Terms of Radius:
The mass m of a loop made from a uniform wire can be expressed in terms of its circumference and linear mass density λ:
m=Circumference⋅λ=2πr⋅λ
Therefore, for loop P (with radius r1):
m1=2πr1⋅λ
and for loop Q (with radius r2):
m2=2πr2⋅λ
3. Calculating the Moments of Inertia:
Now substituting the expressions for mass into the moment of inertia formula:
- For loop P:
I1=m1⋅r21=(2πr1⋅λ)⋅r21=2πλr31
- For loop Q:
I2=m2⋅r22=(2πr2⋅λ)⋅r22=2πλr32
4. Using the Given Relation:
We know from the problem statement that:
I2=4I1
Substituting the expressions we derived:
2πλr32=4⋅(2πλr31)
5. Simplifying the Equation:
We can cancel 2πλ from both sides (assuming λ≠0):
r32=4r31
6. Finding the Ratio of Radii:
To find the ratio r2r1, we take the cube root of both sides:
r2r1=√(3)4
Final Answer:
Thus, the ratio of the radii is:
r2r1=41/3
The moment of inertia I for a circular loop is given by the formula:
I=m⋅r2
where m is the mass of the loop and r is the radius.
The mass m of a loop made from a uniform wire can be expressed in terms of its circumference and linear mass density λ:
m=Circumference⋅λ=2πr⋅λ
Therefore, for loop P (with radius r1):
m1=2πr1⋅λ
and for loop Q (with radius r2):
m2=2πr2⋅λ
Now substituting the expressions for mass into the moment of inertia formula:
- For loop P:
I1=m1⋅r21=(2πr1⋅λ)⋅r21=2πλr31
- For loop Q:
I2=m2⋅r22=(2πr2⋅λ)⋅r22=2πλr32
We know from the problem statement that:
I2=4I1
Substituting the expressions we derived:
2πλr32=4⋅(2πλr31)
We can cancel 2πλ from both sides (assuming λ≠0):
r32=4r31
To find the ratio r2r1, we take the cube root of both sides:
r2r1=√(3)4
Thus, the ratio of the radii is:
r2r1=41/3
Similar Questions
Two loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
View SolutionConsider two uniform discs of the same thickness and different radii R1=R and R2=αR made of the same material. If the ratio of their moments of inertia I1andI2, respectively, about their axes is I1:I2=1:16 then the value of α is :
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
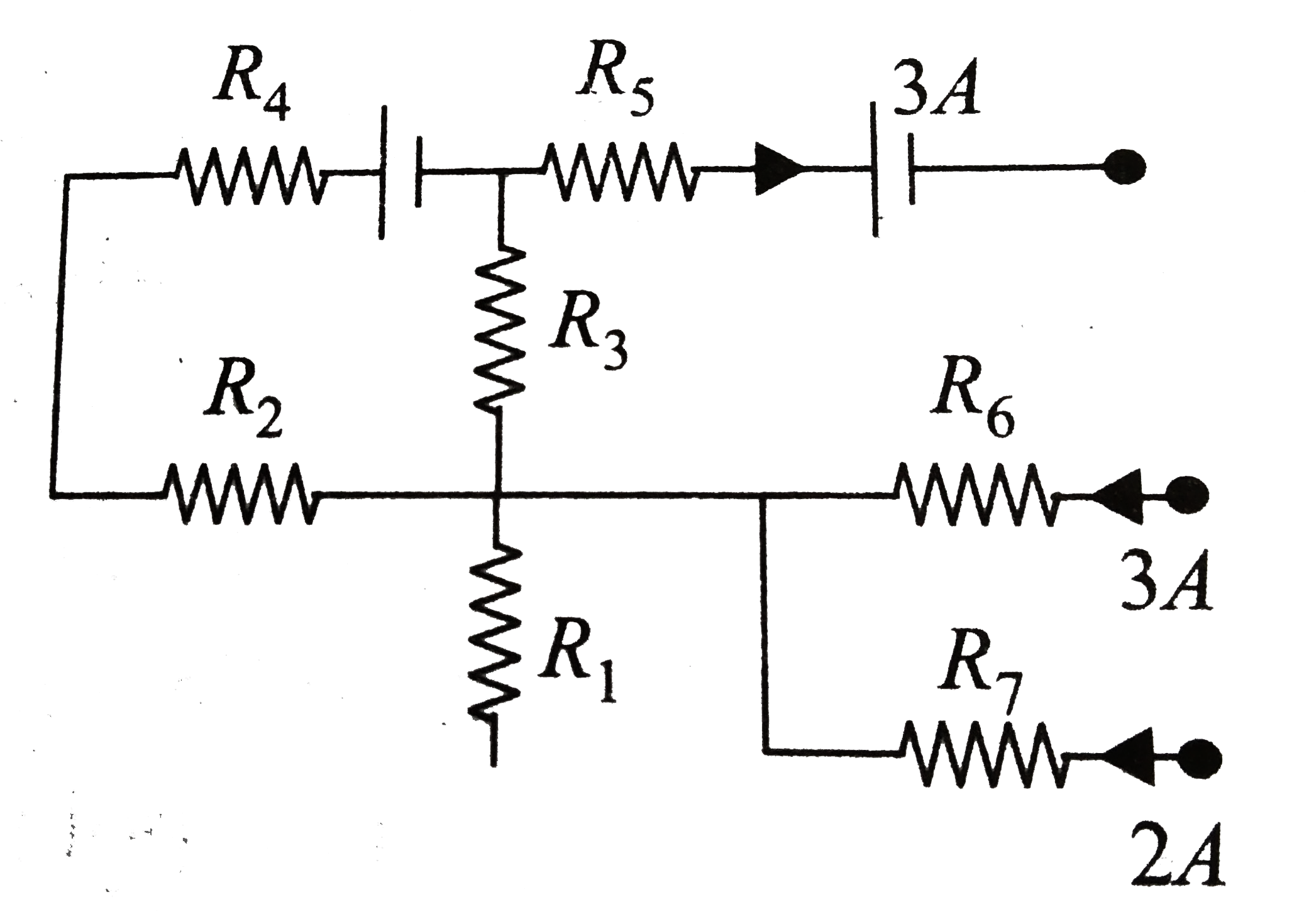 .
.
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo bodies with moment of inertia I1 and I2(I1>I2) have equal angular momenta. If their kinetic energy of rotation are E1 and E2 respectively, then.
View SolutionTwo circular loops A and B of radii R and 2R respectively are made of the similar wire. Their moments of inertia about the axis passing through the centre of perpendicular to their plane are IA and IB respectively. The ratioIAIB is :
View SolutionTwo plane circular coilds P and Q have radii r1 and r2, respectively, (r1<<r2) and are coaxial as shown in fig. The number of turns in P and Q are respectively N1 and N2. If current in coil Q is varied steadily at a rate x ampere/second then the induced emf in the coil P will be approximatery -
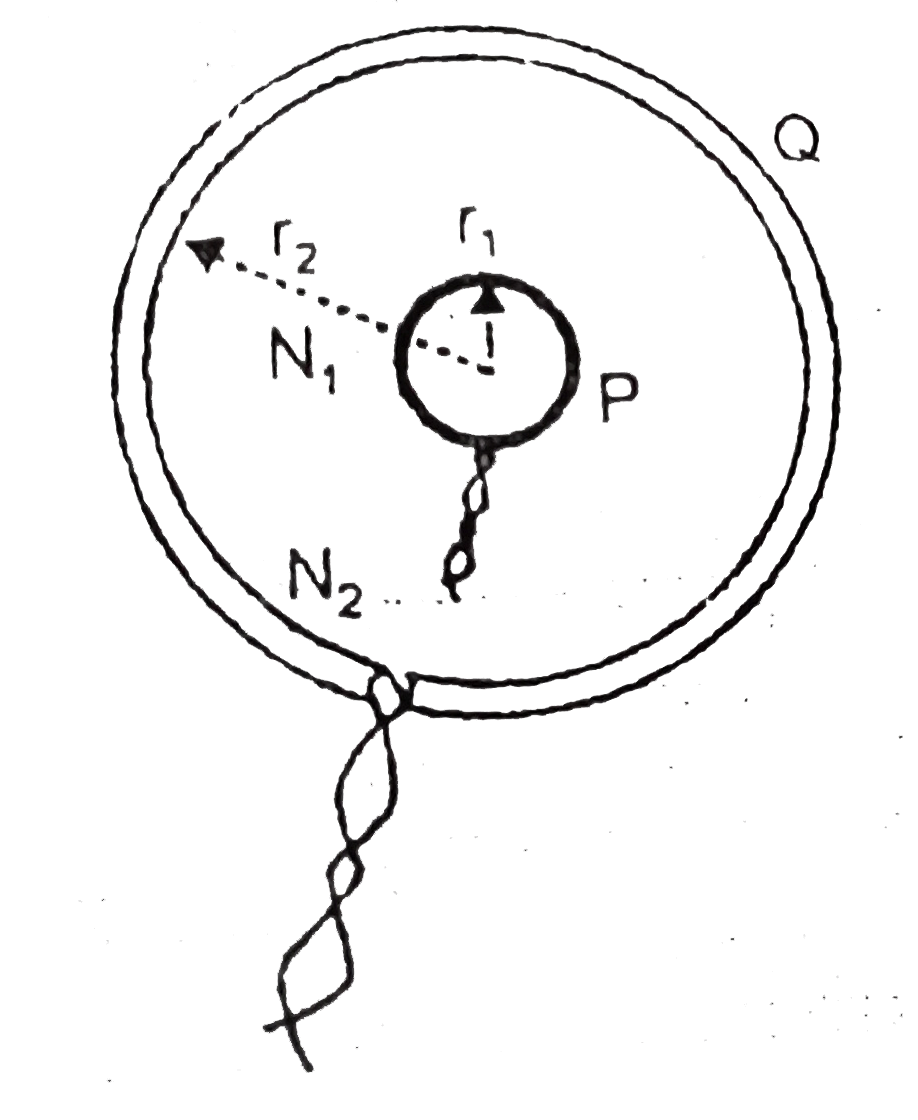
View SolutionTwo circular coils P & Q are coaxially & carry currents I1 and I2 respectively (all direction are w.r.t. the observer)

View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View Solution