An ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
The word done by the gas is less when it is expanded reversibly from V1 to V2 under adiabatic conditions as compared to that when expanded reversibly from V1 to V2 under isothermal conditions
The change in internal energy of the gas is (i) zero, if it is expanded reversibly with T1=T2 and (ii) positive, if it is exapnded reversibly under adiabatic conditions with T1≠T2
If the expansion is carried out freely, it is simultaneously both isothermal as well as adiabatic
The work done on the gas is maximum when it is compressed irreversibly from (p2,V2) to (p1,V1) against constant pressure p1
The correct Answer is:B
To solve the problem regarding the expansion of an ideal gas from (p1, V1, T1) to (p2, V2, T2) under different conditions, we need to analyze the statements provided and determine their validity based on the principles of thermodynamics.
Step 1: Analyze the Work Done in Different Processes
- Isothermal Process: In an isothermal expansion, the temperature remains constant (T1 = T2). The work done by the gas can be calculated using the formula:
Wiso=nRTln(V2V1)
Here, the work done is positive as the gas expands.
- Adiabatic Process: In an adiabatic expansion, there is no heat exchange (Q = 0). The work done can be expressed as:
Wadi=p2V2−p1V1γ−1
where γ is the heat capacity ratio (C_p/C_v). The work done here is less than that in the isothermal process because the internal energy change is also involved.
Conclusion: The work done during adiabatic expansion is less than that during isothermal expansion. Thus, the first statement is correct.
Step 2: Change in Internal Energy
- Internal Energy Change in Isothermal Process: For an ideal gas, the change in internal energy (ΔU) depends only on temperature. Since T1 = T2 in an isothermal process, ΔU = 0.
- Internal Energy Change in Adiabatic Process: In an adiabatic process, since there is no heat exchange, the change in internal energy is equal to the work done on or by the gas. If the gas expands, work is done by the gas, and thus ΔU is negative.
Conclusion: The first part of the statement regarding ΔU being zero in isothermal expansion is correct, while the second part regarding ΔU being positive in adiabatic expansion is incorrect. Therefore, the second statement is partially correct.
Step 3: Free Expansion
- In free expansion, the gas expands against a vacuum (p_external = 0). No work is done (W = 0), and since there is no heat exchange, ΔU = Q = 0.
- In this case, the process can be considered both isothermal (if the gas does not change temperature) and adiabatic (since there is no heat transfer).
Conclusion: The statement that free expansion is simultaneously both isothermal and adiabatic is correct.
Step 4: Work Done in Compression
- When compressing a gas irreversibly from (p2, V2) to (p1, V2) against a constant pressure (p1), the work done is calculated differently than in a reversible process.
- In irreversible processes, the work done is generally less than that in a reversible process due to the path taken.
Conclusion: The statement that the work done on the gas is maximum during irreversible compression is incorrect.
Final Conclusion
The correct statements are:
- A: Correct (Work done in adiabatic expansion is less than in isothermal)
- C: Correct (Free expansion is both isothermal and adiabatic)
- D: Incorrect (Work done in irreversible processes is not maximum)
Thus, the correct options are A and C.
- Isothermal Process: In an isothermal expansion, the temperature remains constant (T1 = T2). The work done by the gas can be calculated using the formula:
Wiso=nRTln(V2V1)
Here, the work done is positive as the gas expands.
Wadi=p2V2−p1V1γ−1
where γ is the heat capacity ratio (C_p/C_v). The work done here is less than that in the isothermal process because the internal energy change is also involved.
- Internal Energy Change in Isothermal Process: For an ideal gas, the change in internal energy (ΔU) depends only on temperature. Since T1 = T2 in an isothermal process, ΔU = 0.
- In free expansion, the gas expands against a vacuum (p_external = 0). No work is done (W = 0), and since there is no heat exchange, ΔU = Q = 0.
- When compressing a gas irreversibly from (p2, V2) to (p1, V2) against a constant pressure (p1), the work done is calculated differently than in a reversible process.
The correct statements are:
- A: Correct (Work done in adiabatic expansion is less than in isothermal)
- C: Correct (Free expansion is both isothermal and adiabatic)
- D: Incorrect (Work done in irreversible processes is not maximum)
Similar Questions
Knowledge Check
Starting from the same initial conditions, an ideal gas expands from volume V1→V2 in three different ways. The work done by the gas is W1 if he process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic. Then
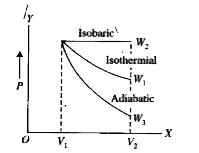 AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
A gas with cpcV=γ goes from an intial state (p1,V1,T1) to a final state (p2,V2,T2) through an adiabatic process. The work done by the gas is
View SolutionOne mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path A?
View SolutionFor an ideal gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path A?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
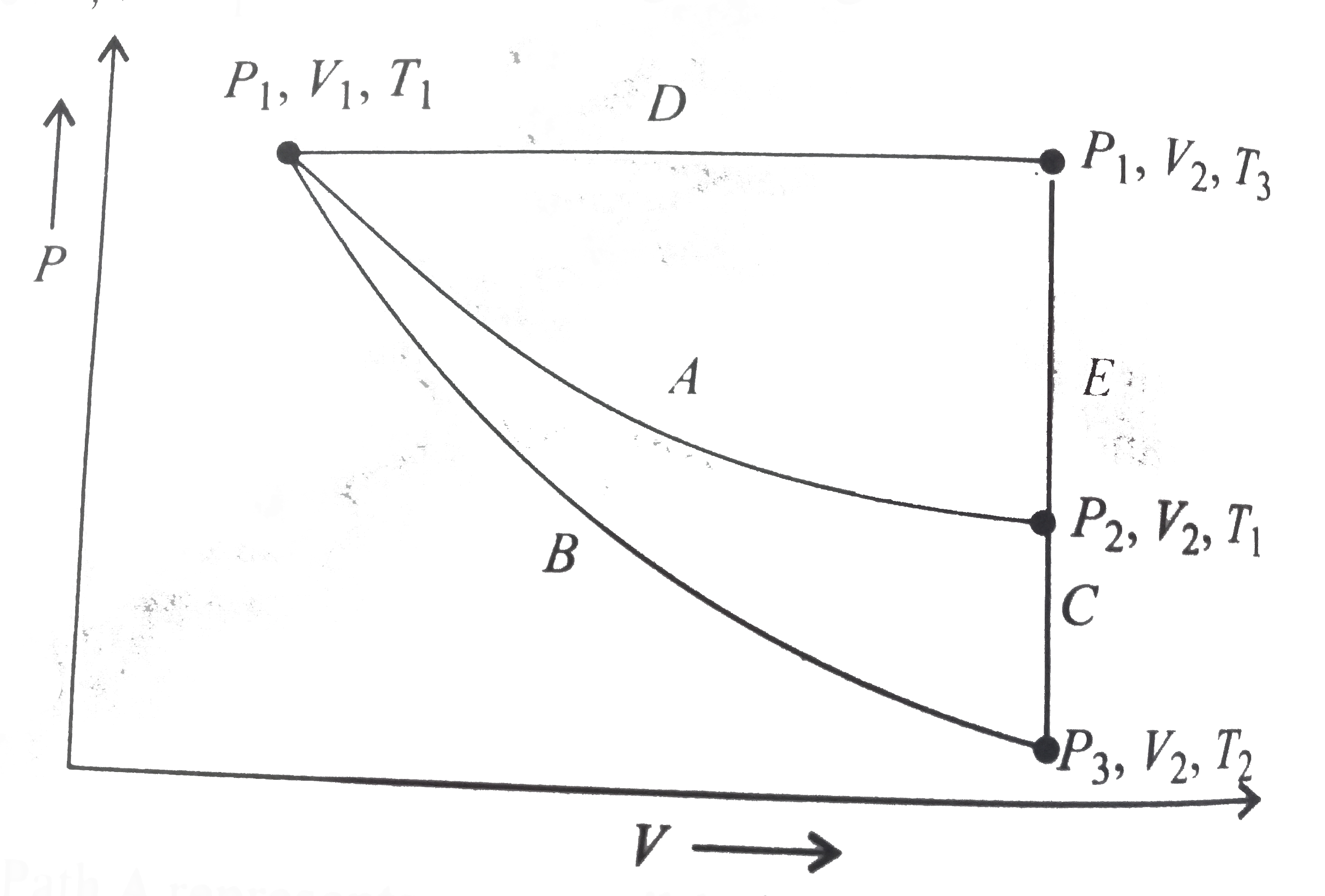
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
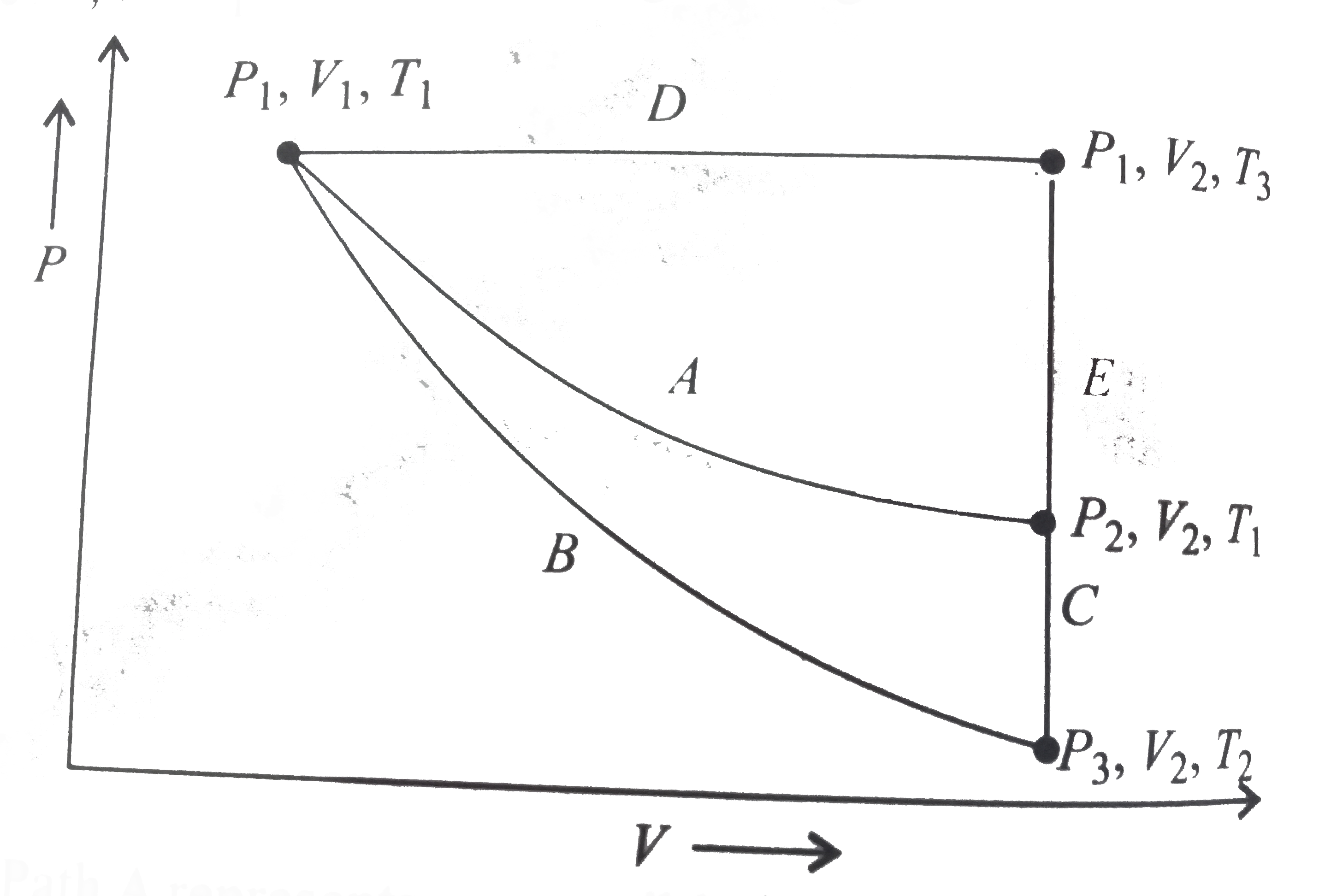
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
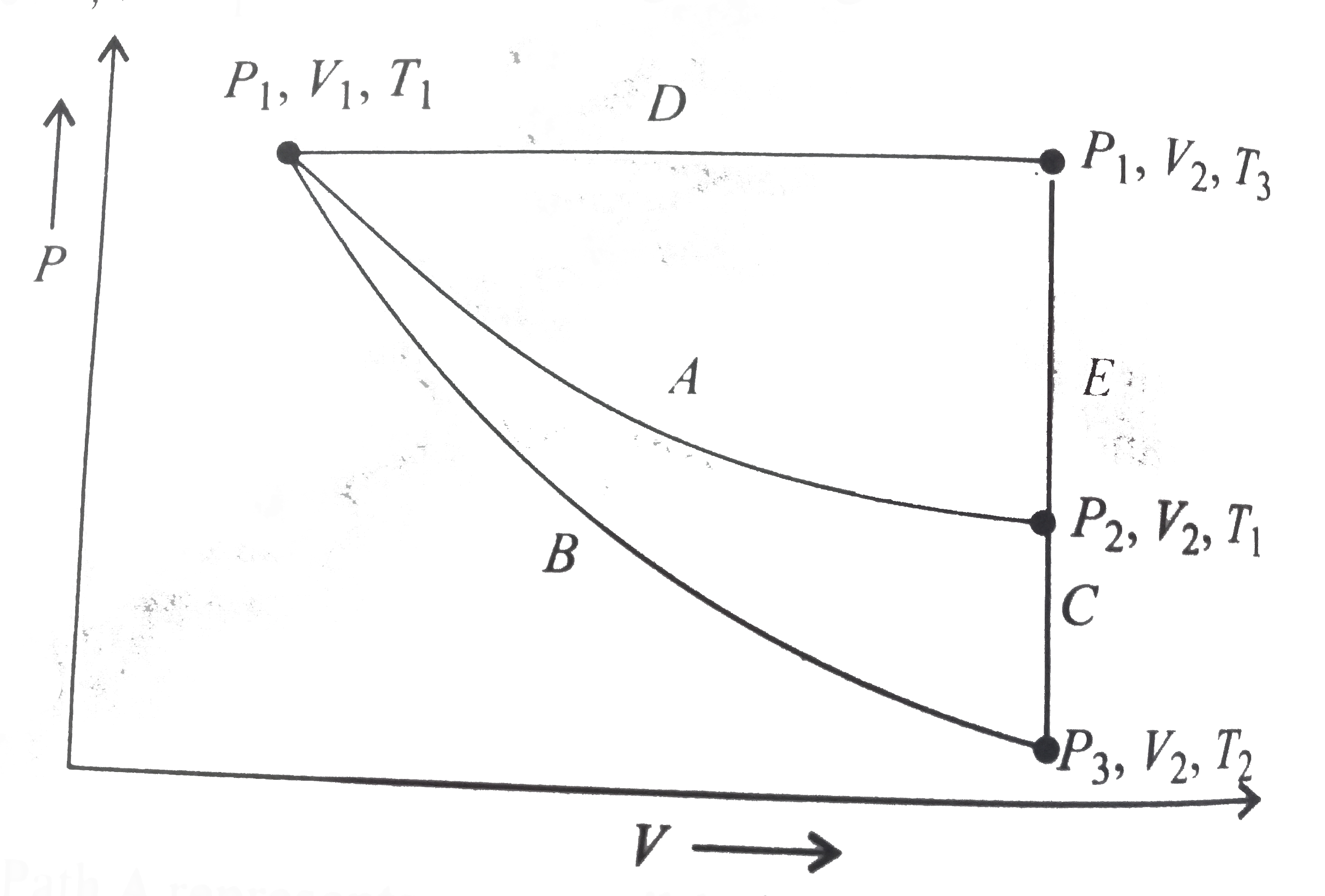
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is ΔS for path (D+E)?
View Solution
