In a region of uniform electric field ofn intencity E, an electron of mass me is released from rest. The distance travelled by the eloctron in a time t is
2met2e
eEt22me
megt2eE
2Et2eme
The correct Answer is:B
To solve the problem step-by-step, we will follow the principles of physics related to electric fields and motion.
Step 1: Identify the forces acting on the electron
The electron is placed in a uniform electric field E. The force F acting on the electron due to the electric field can be expressed as:
F=qE
where q is the charge of the electron. The charge of the electron is −e (where e is the elementary charge). Thus, the force acting on the electron is:
F=−eE
Step 2: Relate force to acceleration
According to Newton's second law, the force acting on an object is also equal to the product of its mass and acceleration:
F=mea
where me is the mass of the electron and a is its acceleration. Setting the two expressions for force equal gives:
mea=−eE
From this, we can solve for the acceleration a:
a=−eEme
Step 3: Use kinematic equations to find the distance traveled
The electron is released from rest, which means its initial velocity u=0. We can use the kinematic equation for distance s traveled under constant acceleration:
s=ut+12at2
Substituting u=0 into the equation gives:
s=12at2
Now, substituting the expression for acceleration a:
s=12(−eEme)t2
This simplifies to:
s=−eE2met2
Step 4: Interpret the result
The negative sign indicates that the electron moves in the direction opposite to the electric field due to its negative charge. However, for the distance traveled, we can express it as:
s=eE2met2
Final Answer
The distance traveled by the electron in time t is:
s=eE2met2
The electron is placed in a uniform electric field E. The force F acting on the electron due to the electric field can be expressed as:
F=qE
where q is the charge of the electron. The charge of the electron is −e (where e is the elementary charge). Thus, the force acting on the electron is:
F=−eE
According to Newton's second law, the force acting on an object is also equal to the product of its mass and acceleration:
F=mea
where me is the mass of the electron and a is its acceleration. Setting the two expressions for force equal gives:
mea=−eE
From this, we can solve for the acceleration a:
a=−eEme
The electron is released from rest, which means its initial velocity u=0. We can use the kinematic equation for distance s traveled under constant acceleration:
s=ut+12at2
Substituting u=0 into the equation gives:
s=12at2
Now, substituting the expression for acceleration a:
s=12(−eEme)t2
This simplifies to:
s=−eE2met2
The negative sign indicates that the electron moves in the direction opposite to the electric field due to its negative charge. However, for the distance traveled, we can express it as:
s=eE2met2
The distance traveled by the electron in time t is:
s=eE2met2
Similar Questions
In a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schmatic and not drawn to scale]
View SolutionIn a region of space uniform electric field is present as →E=E0ˆi and uniform magnetci field is present as →B=−B0ˆj . An electron is released from rest at origin. What is the path followed by electron after released. (E0&B0are positive constants )
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA charged particle having charge q and mass m moves rectilinearly under the action of the electric field E(x)=(4−3x)N/C where x is the distance was initially at rest. The distance travelled by the particle till it comes instantaneously to rest again for the first time, is
View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionA particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
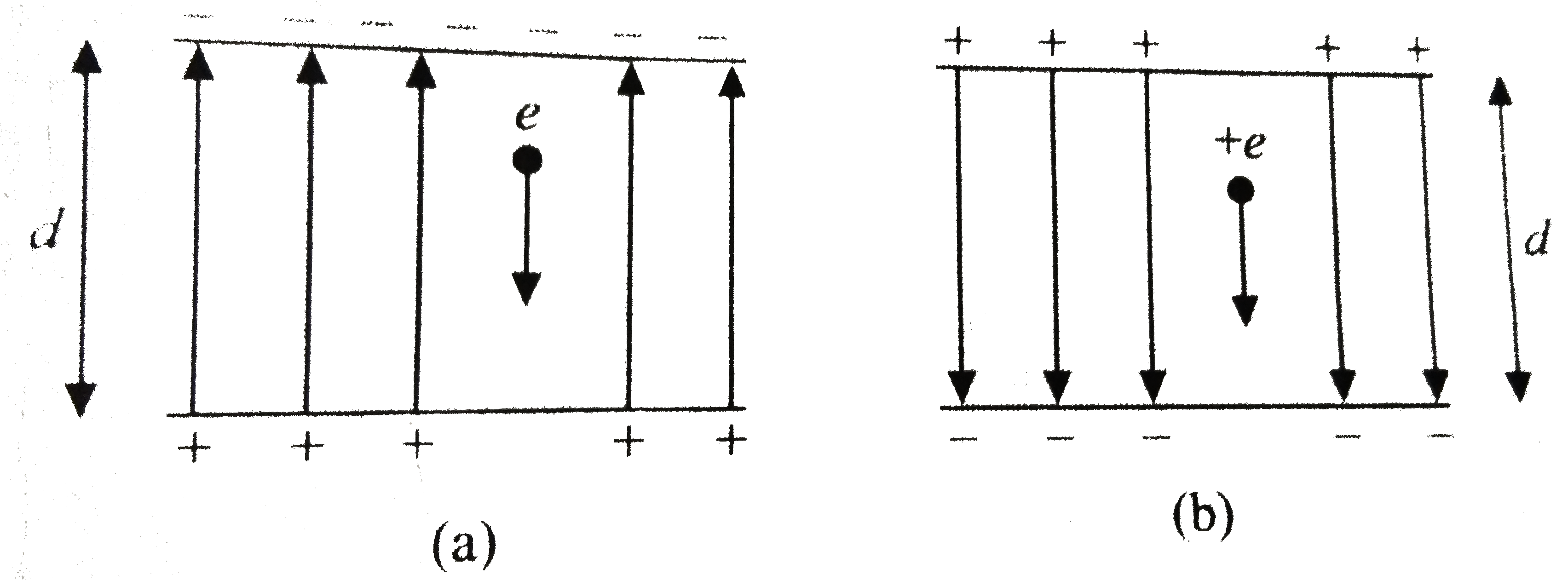 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
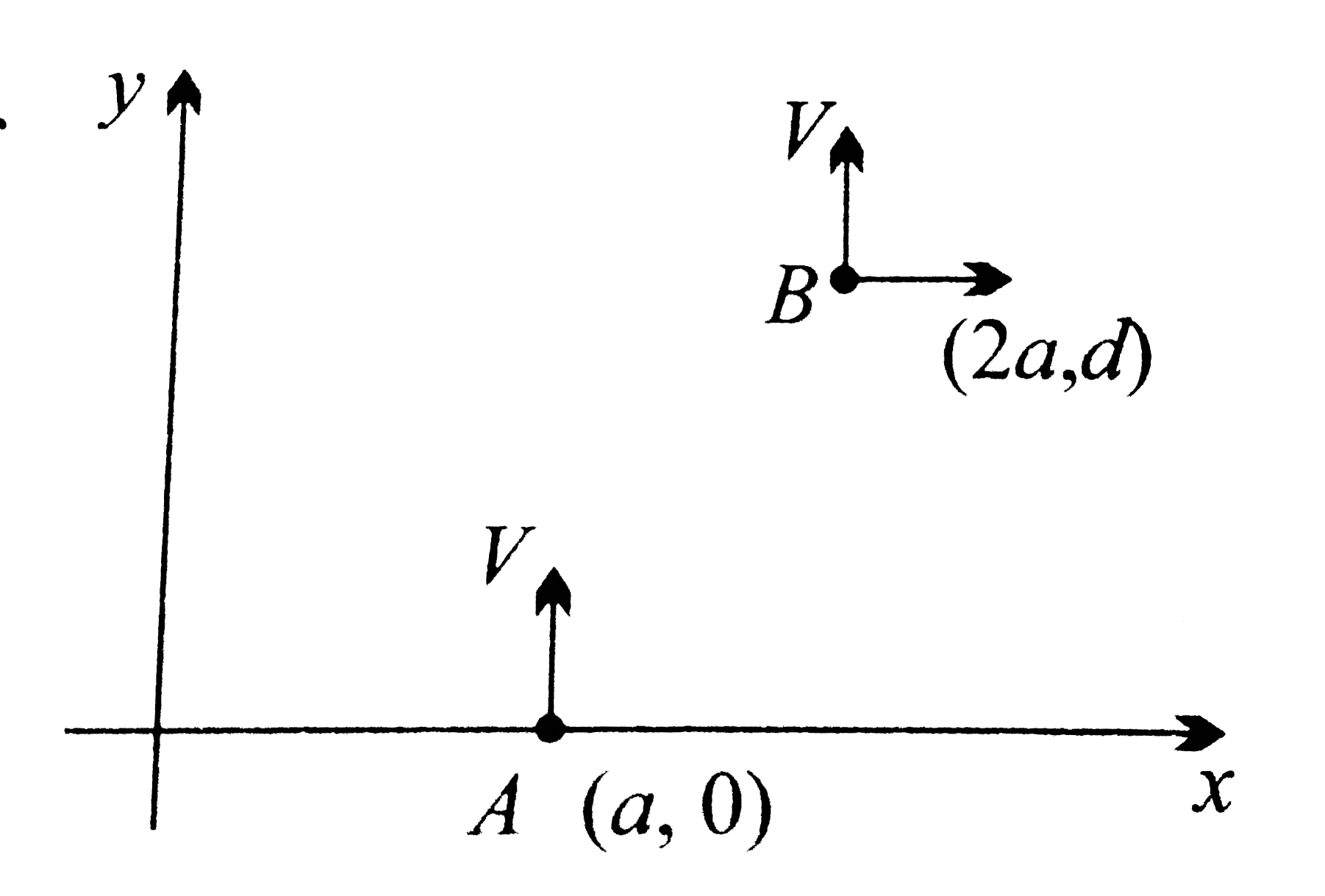 .
.
Find electric field.
View Solution
