A particle of mass m and charge −q is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its potential energy on the distance x travelled by it is correctly given by (assume initial potential energy to be zero ,graphs are schematic and not drawn to scale)
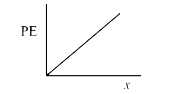

The correct Answer is:B
To solve the problem, we need to analyze the behavior of a charged particle in a uniform electric field and how its potential energy changes as it moves.
1. Understanding the System:
- We have a particle with mass m and charge −q in a uniform electric field E.
- The electric field exerts a force on the particle given by F=qE. Since the charge is negative, the force will act in the opposite direction of the electric field.
2. Force on the Particle:
- The force acting on the particle is F=−qE.
- If we assume the electric field is directed in the positive x-direction, then the force on the particle will be in the negative x-direction.
3. Work Done by the Electric Field:
- The work done W by the electric field when the particle moves a distance x is given by:
W=F⋅d=(−qE)(−x)=qEx
- Here, d is the displacement vector in the direction of the movement.
4. Change in Potential Energy:
- The change in potential energy ΔU is related to the work done by the conservative force:
ΔU=−W
- Substituting the expression for work done:
ΔU=−qEx
5. Initial Potential Energy:
- We are given that the initial potential energy Ui=0. Therefore, the final potential energy Uf is:
Uf=Ui+ΔU=0−qEx=−qEx
6. Dependence of Potential Energy on Distance:
- The final expression for potential energy as a function of distance x is:
U(x)=−qEx
- This shows that the potential energy decreases linearly with increasing x since the coefficient of x is negative.
7. Graphical Representation:
- The graph of potential energy U versus distance x will be a straight line with a negative slope, indicating that as x increases, U decreases.
Conclusion:
The dependence of potential energy on the distance x travelled by the particle is given by:
U(x)=−qEx
This indicates a linear decrease in potential energy with distance.
- We have a particle with mass m and charge −q in a uniform electric field E.
- The electric field exerts a force on the particle given by F=qE. Since the charge is negative, the force will act in the opposite direction of the electric field.
- The force acting on the particle is F=−qE.
- If we assume the electric field is directed in the positive x-direction, then the force on the particle will be in the negative x-direction.
- The work done W by the electric field when the particle moves a distance x is given by:
W=F⋅d=(−qE)(−x)=qEx
- Here, d is the displacement vector in the direction of the movement.
- The change in potential energy ΔU is related to the work done by the conservative force:
ΔU=−W
- Substituting the expression for work done:
ΔU=−qEx
- We are given that the initial potential energy Ui=0. Therefore, the final potential energy Uf is:
Uf=Ui+ΔU=0−qEx=−qEx
- The final expression for potential energy as a function of distance x is:
U(x)=−qEx
- This shows that the potential energy decreases linearly with increasing x since the coefficient of x is negative.
- The graph of potential energy U versus distance x will be a straight line with a negative slope, indicating that as x increases, U decreases.
The dependence of potential energy on the distance x travelled by the particle is given by:
U(x)=−qEx
This indicates a linear decrease in potential energy with distance.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 26 (2020)EXERCISE - PHYSICS (SECTION 2)5videos
JEE MAIN REVISION TEST - 26 (2020)
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 25 | JEE - 2020EXERCISE - PHYSICS25videos
JEE MAIN REVISION TEST - 25 | JEE - 2020
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 27 - JEE -2020EXERCISE - PHYSICS (SECTION 2)5videos
JEE MAIN REVISION TEST - 27 - JEE -2020
Similar Questions
A particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA particle of mass and charge is released from rest in a uniform electric field. If there is no other force on the particle, the dependence of its kinetic energy on the distance travelled by it is correctly given by (graphs are schematic and not drawn to scale)
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains after moving a distance y between the plates.
View SolutionIn a uniform electric field, a point charge of mass m and charge q is released from rest. If there are no other forces acting on the particle, then which of the following graphs, correctly show the dependence of the particles speed v on the distance x travelled by the particles speed v on the distance x travelled by it? [Graphs are schmatic and not drawn to scale]
View SolutionA positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge.
View Solution

