Sixty four identical sphere of change q and capacitance C each are combined to form a large sphere . The charge and capacitance of the large sphere is
64 q, C
16 q, 4 C
64 q, 4 C
16 q , 64 C
The correct Answer is:C
To solve the problem of finding the charge and capacitance of a large sphere formed by combining 64 identical smaller spheres, we can follow these steps:
Step 1: Understand the Given Information
We have 64 identical spheres, each with a charge q and capacitance C. We need to find the charge and capacitance of the larger sphere formed by combining these smaller spheres.
Step 2: Calculate the Total Charge
The total charge Q on the larger sphere can be calculated by using the principle of conservation of charge. Since there are 64 spheres, each with charge q, the total charge is:
Q=64q
Step 3: Calculate the Radius of the Large Sphere
Let the radius of each smaller sphere be r. The volume of one smaller sphere is given by:
Vsmall=43πr3
The total volume of the 64 smaller spheres is:
Vtotal=64×Vsmall=64×43πr3=2563πr3
This total volume is equal to the volume of the larger sphere with radius R:
Vlarge=43πR3
Setting the two volumes equal gives:
2563πr3=43πR3
Cancelling 43π from both sides, we get:
256r3=4R3
Dividing both sides by 4:
64r3=R3
Taking the cube root of both sides:
R=4r
Step 4: Calculate the Capacitance of the Large Sphere
The capacitance C of a sphere is given by:
C=4πϵ0R
Substituting R=4r:
C′=4πϵ0(4r)=16πϵ0r
Since the capacitance of the smaller sphere is C=4πϵ0r, we can express C′ in terms of C:
C′=16πϵ0r=4C
Final Results
- The charge of the large sphere is Q=64q.
- The capacitance of the large sphere is C′=4C.
Summary
Thus, the charge and capacitance of the large sphere formed by combining 64 identical smaller spheres are:
- Charge: 64q
- Capacitance: 4C
We have 64 identical spheres, each with a charge q and capacitance C. We need to find the charge and capacitance of the larger sphere formed by combining these smaller spheres.
The total charge Q on the larger sphere can be calculated by using the principle of conservation of charge. Since there are 64 spheres, each with charge q, the total charge is:
Q=64q
Let the radius of each smaller sphere be r. The volume of one smaller sphere is given by:
Vsmall=43πr3
The total volume of the 64 smaller spheres is:
Vtotal=64×Vsmall=64×43πr3=2563πr3
This total volume is equal to the volume of the larger sphere with radius R:
Vlarge=43πR3
Setting the two volumes equal gives:
2563πr3=43πR3
Cancelling 43π from both sides, we get:
256r3=4R3
Dividing both sides by 4:
64r3=R3
Taking the cube root of both sides:
R=4r
The capacitance C of a sphere is given by:
C=4πϵ0R
Substituting R=4r:
C′=4πϵ0(4r)=16πϵ0r
Since the capacitance of the smaller sphere is C=4πϵ0r, we can express C′ in terms of C:
C′=16πϵ0r=4C
- The charge of the large sphere is Q=64q.
- The capacitance of the large sphere is C′=4C.
Thus, the charge and capacitance of the large sphere formed by combining 64 identical smaller spheres are:
- Charge: 64q
- Capacitance: 4C
Similar Questions
1000 small water drops each of capacitance C join togethter to form one large spherical drop. The capacitance of bigge sphere is
View SolutionSixty four spherical drops each of radius 2cm and carrying 5C charge combine to form a bigger drop. Its capacity is.
View SolutionTwo identical conducting spheres are charged by induction and then separated by a large distance, sphere 1 has charge +Q and sphere 2 has charge -Q. A third sphere is initially uncharged. If sphere 3 is touched to sphere 1 and separated and then touched to sphere 2 and separated what is the final charge on each of the three spheres?
View SolutionIf the circumference of a sphere is 2 m, then capacitance of sphere in water would be
View SolutionConsider three identical metal spheres A,B and C. Sphere A carries charge +6q, sphere B carries charge −3q and sphere C carries no charge . Spheres A and B are touched together and then separated. Sphere C is then touched to sphere A and separated from it . Finally the sphere C is touched to sphere B and separated from it . Find the final charge on the sphere C.
View SolutionAn isolated conducting sphere of charge Q and radius R is connected to a similar uncharged sphere (kept at a large distance) by using a high resistance wire. After a long time is the amount of heat loss?
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
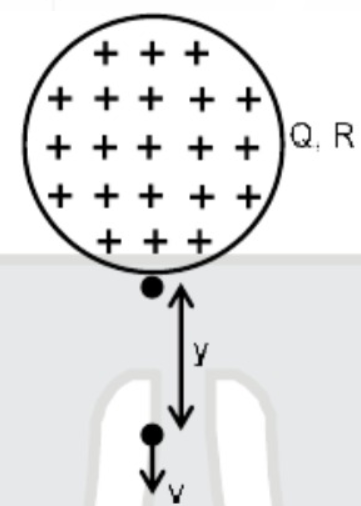
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA sphere of radius 0.03m is suspended within a hollow sphere of radius 0.05m. If the inner sphere is charged to a potential of 1500 volt and outer sphere is earthed. Find the capacitance and the charge of the inner sphere.
View SolutionTwo metal spheres of radii a and b are connected by a thin wire. Their separation is very large compared to their dimensions. The capacitance of this system is
View Solution
