Volume - temperature graph at atmospheric pressure for a monatomic gas ( V in m3 , T in Celsius ) is
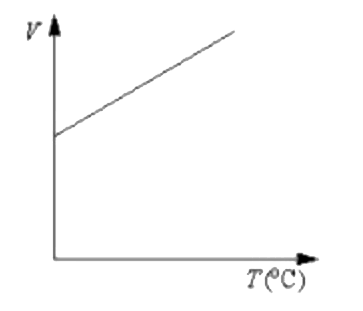

The correct Answer is:B
To solve the problem of determining the volume-temperature graph for a monatomic gas at atmospheric pressure, we can follow these steps:
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the absolute temperature in Kelvin.
2. Convert Temperature to Celsius:
Since the temperature is given in Celsius, we need to convert it to Kelvin. The conversion is:
T(K)=T(°C)+273
3. Rearrange the Ideal Gas Law:
We need to express volume V in terms of temperature T:
V=nRPT
Substituting T with (T(°C)+273):
V=nRP(T(°C)+273)
4. Identify the Linear Equation:
The equation can be rewritten in the form of y=mx+c:
V=nRPT(°C)+nR⋅273P
Here, y is V, x is T(°C), m=nRP (the slope), and c=nR⋅273P (the y-intercept).
5. Determine the Characteristics of the Graph:
- The slope m is positive since n, R, and P are all positive.
- The y-intercept c is positive because it is a product of positive constants and 273.
6. Analyze the Options:
Based on the characteristics of the graph:
- The graph should have a positive slope and a positive y-intercept.
7. Conclusion:
The correct graph for the volume-temperature relationship of a monatomic gas at atmospheric pressure is the one that shows a straight line with a positive slope and a positive intercept.
The ideal gas law is given by the equation:
PV=nRT
where P is the pressure, V is the volume, n is the number of moles, R is the gas constant, and T is the absolute temperature in Kelvin.
Since the temperature is given in Celsius, we need to convert it to Kelvin. The conversion is:
T(K)=T(°C)+273
We need to express volume V in terms of temperature T:
V=nRPT
Substituting T with (T(°C)+273):
V=nRP(T(°C)+273)
The equation can be rewritten in the form of y=mx+c:
V=nRPT(°C)+nR⋅273P
Here, y is V, x is T(°C), m=nRP (the slope), and c=nR⋅273P (the y-intercept).
- The slope m is positive since n, R, and P are all positive.
- The y-intercept c is positive because it is a product of positive constants and 273.
Based on the characteristics of the graph:
- The graph should have a positive slope and a positive y-intercept.
The correct graph for the volume-temperature relationship of a monatomic gas at atmospheric pressure is the one that shows a straight line with a positive slope and a positive intercept.
Similar Questions
At a given volume and temperature the pressure of a gas
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View SolutionVolume occupied by an ideal gas at one atmospheric pressure and 0∘C is V ml. Its volume at 273 K will be
View SolutionA certain amount of a gas at 27∘C and 1 atmospheric pressure occupies a volume of 25dm3. If the pressure is kept constant and the temperature is raised to 77∘C, what would be the volume of the gas ?
View SolutionThe volume-temperature graphs of a given mass of an ideal gas at constant pressure are shown below. What is the correct order of pressure ?

View SolutionA plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in figure. Which of the following order of pressure is correct for this gas ?

View SolutionA plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin . The plots at different values of pressure are shown in figure .
Which of the following order of pressure is correct for this gas ?

View SolutionA plot of volume (V) versus temperature (T) for a gas at constannt pressure is a straight line passing through the origin. The plots at different values of pressure are shown in figure. Which of the following order of pressure is correct for this gas?

View SolutionUnit mass of liquid of volume V1 completely turns into a gas of volume V2 at constant atmospheric pressure P and temperature T. The latent heat of vaporization is "L". Then the change in internal energy of the gas is
View SolutionThe pressure P, Volume V and temperature T of a gas in the jar A and the other gas in the jar B at pressure 2P, volume V/4 and temperature 2T, then the ratio of the number of molecules in the jar A and B will be
View Solution
