Two circles touch each other at point X, A common tangent touch them at two distinct points Y and Z. If another tangent passing through X cut YZ at A and XA = 16cm, then what is the value (in cm) of YZ?
दो वृत्त एक-दूसरे को बिन्दु X पर स्पर्श करते है। एक उभय-निष्ठ स्पर्शरेखा उन्हे दो अलग बिन्दुओं Y तथा Z पर स्पर्श करती हैं यदि X से गुजरने वाली एक अन्य स्पर्शरेखा YZ को A पर काटती है तथा XA = 16 से.मी. है, तो YZ का मान (से.मी. में) क्या है?
18
24
16
32
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the Configuration
We have two circles that touch each other at point X. A common tangent touches the circles at points Y and Z. Another tangent from point X intersects the line segment YZ at point A.
Hint: Visualize the circles and the tangents to understand the relationships between the points.
Step 2: Use the Tangent-Secant Theorem
According to the tangent-secant theorem, if a tangent is drawn from an external point to a circle, the lengths of the tangents drawn from that point to the points of tangency are equal.
Let:
- AX be the tangent from point A to point X.
- AY be the tangent from point A to point Y.
- AZ be the tangent from point A to point Z.
Since AX, AY, and AZ are tangents from point A, we have:
- AX = AY
- AX = AZ
Hint: Remember that the lengths of tangents drawn from an external point to a circle are equal.
Step 3: Set Up the Equation
From the above, we can say:
- AY = AX
- AZ = AX
Thus, we can express the total length of YZ in terms of AX:
- YZ = AY + AZ = AX + AX = 2 * AX
Hint: Think about how the lengths of the tangents relate to the total length of YZ.
Step 4: Substitute the Given Value
We are given that AX = 16 cm. Now, substitute this value into the equation:
- YZ = 2 * AX = 2 * 16 cm = 32 cm
Hint: Always substitute the known values into your equations to find the unknowns.
Step 5: Conclusion
The length of YZ is 32 cm.
Final Answer: YZ = 32 cm
We have two circles that touch each other at point X. A common tangent touches the circles at points Y and Z. Another tangent from point X intersects the line segment YZ at point A.
According to the tangent-secant theorem, if a tangent is drawn from an external point to a circle, the lengths of the tangents drawn from that point to the points of tangency are equal.
- AX be the tangent from point A to point X.
- AY be the tangent from point A to point Y.
- AZ be the tangent from point A to point Z.
- AX = AY
- AX = AZ
From the above, we can say:
- AY = AX
- AZ = AX
- YZ = AY + AZ = AX + AX = 2 * AX
We are given that AX = 16 cm. Now, substitute this value into the equation:
- YZ = 2 * AX = 2 * 16 cm = 32 cm
The length of YZ is 32 cm.
Topper's Solved these Questions
Similar Questions
How many three digit numbers are there in which all the digits are odd?
तीन अंको वाली ऐसी कितनी संख्याएँ हैं जिसमें सभी अंक विषम है?
View SolutionThe given pie chart shows the breakup of total number of the employees of a company working in different offices (A, B, C, D and E). Total No. of employees = 2400
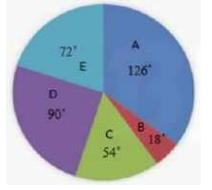 If the percentage of male employees in office C is 20% and that of female employees in E is 40%, then what is the ratio of the number of female employees in C to that of female employees in E?
If the percentage of male employees in office C is 20% and that of female employees in E is 40%, then what is the ratio of the number of female employees in C to that of female employees in E?
View Solutionयदि वृत्त x2+y2=a2 तथा x2+y2−6x−8y+9=0 एक दूसरे को बहिगर्त स्पर्श करते है तो a =
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionदो वृत्त एक दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ की संख्या लिखिये।
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionएक रेखा 'L' परवलय y2=4(x−1) की नाभि से होकर गुजरती है तथा परवलय को दो विभिन्न बिन्दुओं पर प्रतिच्छेद करती है। यदि m रेखा की प्रवणता है, तब
View SolutionCentre of two concentric circles is O. The area of two circles is 616cm^2 and 154 cm^2 respectively. A tangent is drawn through point A on the larger circle to the smaller circle. This tangent touches small circle at B and intersects larger circle at C. What is the length (in cm) of AC? दो संकोंद्रत वृत्त का केन्द्र O है| दोनों वृत्तों का क्षेत्रफल 616 सेमी.^2 तथा- 154 सेमी.^2 है। बडे वृत्त के बिंदु A से छोटे वृत्त पर एक स्पर्श-रेखा खोची गई है यह स्पर्श रेखा छोटे वृत्त को बिंदु B पर स्पर्श करती है तथा बड़े वृत्त को बिंदु C पर प्रतिच्छेद करती है । AC की लम्बाई (सेमी. में) क्या है?
View SolutionPA and PB are two tangents drawn to two cricles of radius 3 cm and 5 cm respectively. PA touches the smaller and larger circles at points X and Y respectively. PB touches the smaller and large circle at point U and V respectively. The centres of the smaller and larger circles are O and N respectively. If ON=12 cm, then what is the value (in cm) of PY? PA तथा PB क्रमश, 3 सेमी. तथा 5 सेमी. वाले दो वृत्तों पर स्पर्श रेखाएँ बनाई गई है। PA छोटे तथा बड़े वृत्त को क्रमशः X तथा Y बिन्दु पर स्पर्श करते है। PB छोटे तथा बड़े वृत्त को U तथा V बिंदु पर स्पर्श करती है। O तथा N क्रमश: छोटे तथा बड़े वृत्त के केन्द्र हैं। यदि ON=12 सेमी. है, तो PY का मान (सेमी. में) क्या है?
View SolutionThree circles of radius 6 cm touches each other externally. Then the distance of the centre of one circle from the line joining the centres of others two circles is equal to: 6 सेमी त्रिज्या वाले तीन वृत्त बाहर से एक-दूसरे को स्पर्श करते हैं तो एक वृत्त के केंद्र की अन्य दो वृत्तों के केंद्रों को जोड़ने वाली रेखा से दूरी कितनी होगी?
View SolutionTwo circles with centres P and Q of radii 7 cm and 3cm, respectively, touch each other externally at a point A. BC is a direct common tangent to these two circles where B and C are the point on the circles respectively. The length of BC is: केंद्र P और Q के साथ दो दो वृत्त, जिनकी त्रिज्याएँ क्रमशः 7 सेमी और 3 सेमी है , एक दूसरे को बाहरी रूप से स्पर्श करते हैं। BC इन दो वृत्त में एक सीधा स्पर्शरेखा है जहां क्रमशः छ और C वृत्त पर बिंदु हैं। BC की लंबाई है
View SolutionTwo circles touch each other externally. The distance between their centres is 8 cm. If the radius of one circle is 3 cm, then the radius of the other circle is: दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं। उनके केंद्रों के बीच की दूरी 8 सेमी है। यदि एक वृत्त की त्रिज्या 3 सेमी है, तो दूसरे वृत्त की त्रिज्या है:
View SolutionIn the figure, two circles with centres P and Q touch externally at R. Tangents AT and BT meet the common tangent TR at T. If AP = 6cm and PT = 10 cm, then BT =? दी गयी आकृति में, दो वृत्त जिनके केंद्र P तथा Q हैं, वे एक-दूसरे को बाहर से R पर स्पर्श करते हैं | स्पर्श रेखाएँ AT तथा BT उभयनिष्ठ स्पर्श रेखा TR से T पर मिलती हैं | यदि AP= 6 सेमी तथा PT = 10 सेमी है, तो BT =?
View SolutionTwo circles of radii 8 cm and 6 cm touch each other externally. The length of the direct common tangent is: 8 सेमी तथा 6 सेमी त्रिज्याओं वाले दो वृत्त एक-दूसरे को बाहर से स्पर्श करते हैं | प्रत्यक्ष उभयनिष्ठ स्पर्श रेखा की लंबाई कितनी है ?
View Solution
