PQ is a tangent to a circle with centre O at the point P. If ΔOPQ is an isoceless triangle, then ∠OQP is equal to
Step by step video & image solution for PQ is a tangent to a circle with centre O at the point P. If DeltaOPQ is an isoceless triangle, then /_OQP is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
PQ is a tangent to a circle with centre O at the point P . If OPQ is an isosceles triangle, then ∠OQP is equal to 30o (b) 45o (c) 60o (d) 90o
View SolutionIf two tangents are inclined at 60∘ are drawn to a circle of radius 3cm then find length of each tangent.
OR
PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
View Solution
Knowledge Check
AB and AC are tangents to the circle with centre O. Then x equals.
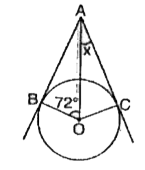 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘If tangent PA and PB from a point P to a circle with centre O are inclined to each other at angle 80∘, then ∠POA is equal to
A50∘B60∘C70∘D80∘If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 70∘, then ∠POA is equal to
A70∘B55∘C100∘D40∘
In figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

View SolutionIn figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
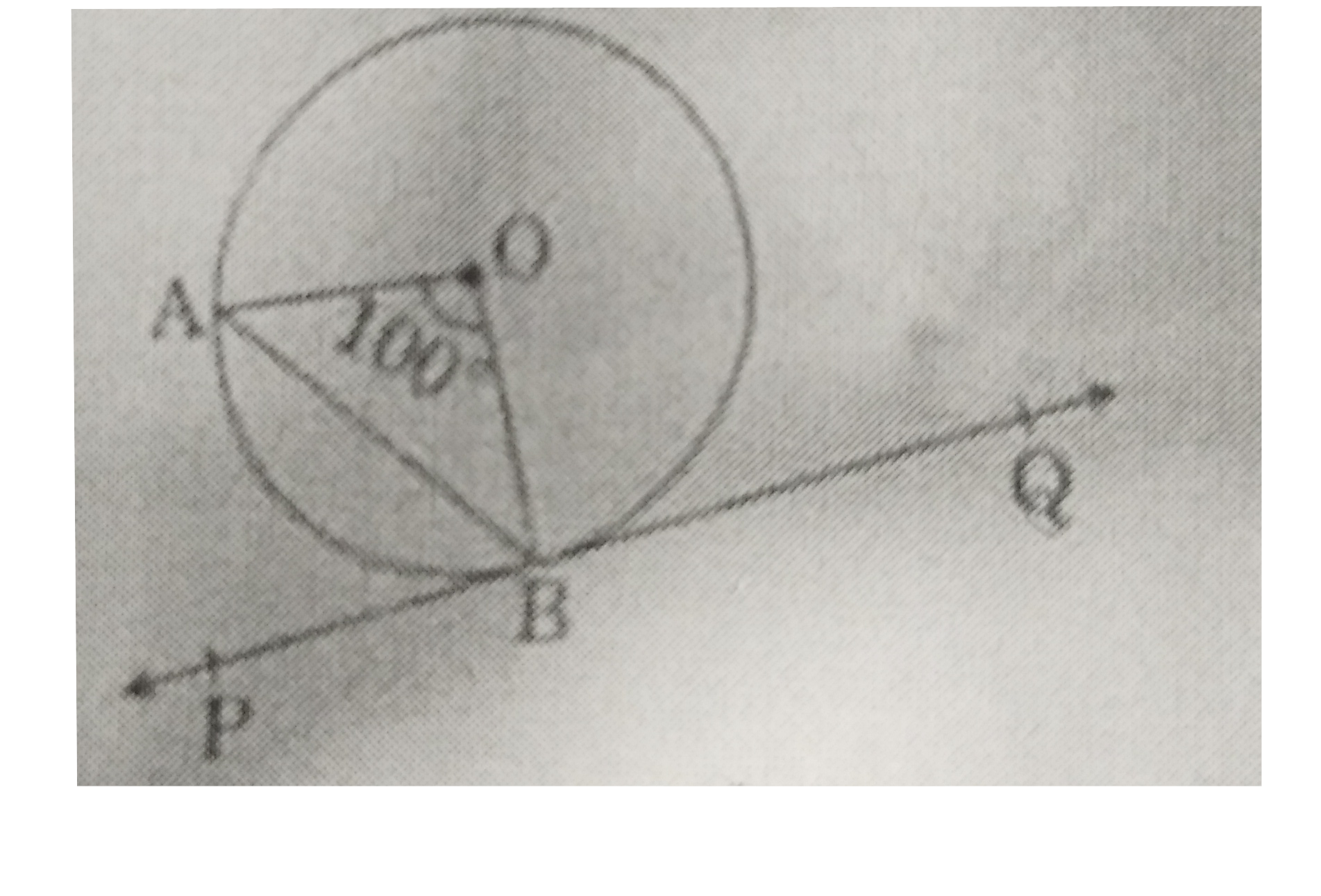
View SolutionIf tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80∘, then ∠POA is equal to
View SolutionPA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
View Solution
