Using distance formula, prove the apollonius' theorem that is in ΔABC,AB2+AC2=2(AD2+BD20) , where D is the middle point of BC.
Video Solution
|
Answer
Step by step video solution for Using distance formula, prove the apollonius' theorem that is in DeltaABC,AB^2+AC^2=2(AD^2+BD^20) , where D is the middle point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check

In the figure, A, B, C and D are points on a line in the order. If AC = 5 , BD = 10 and AD = 13, then what is the length of BC ?A2B8C15D18
In a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.
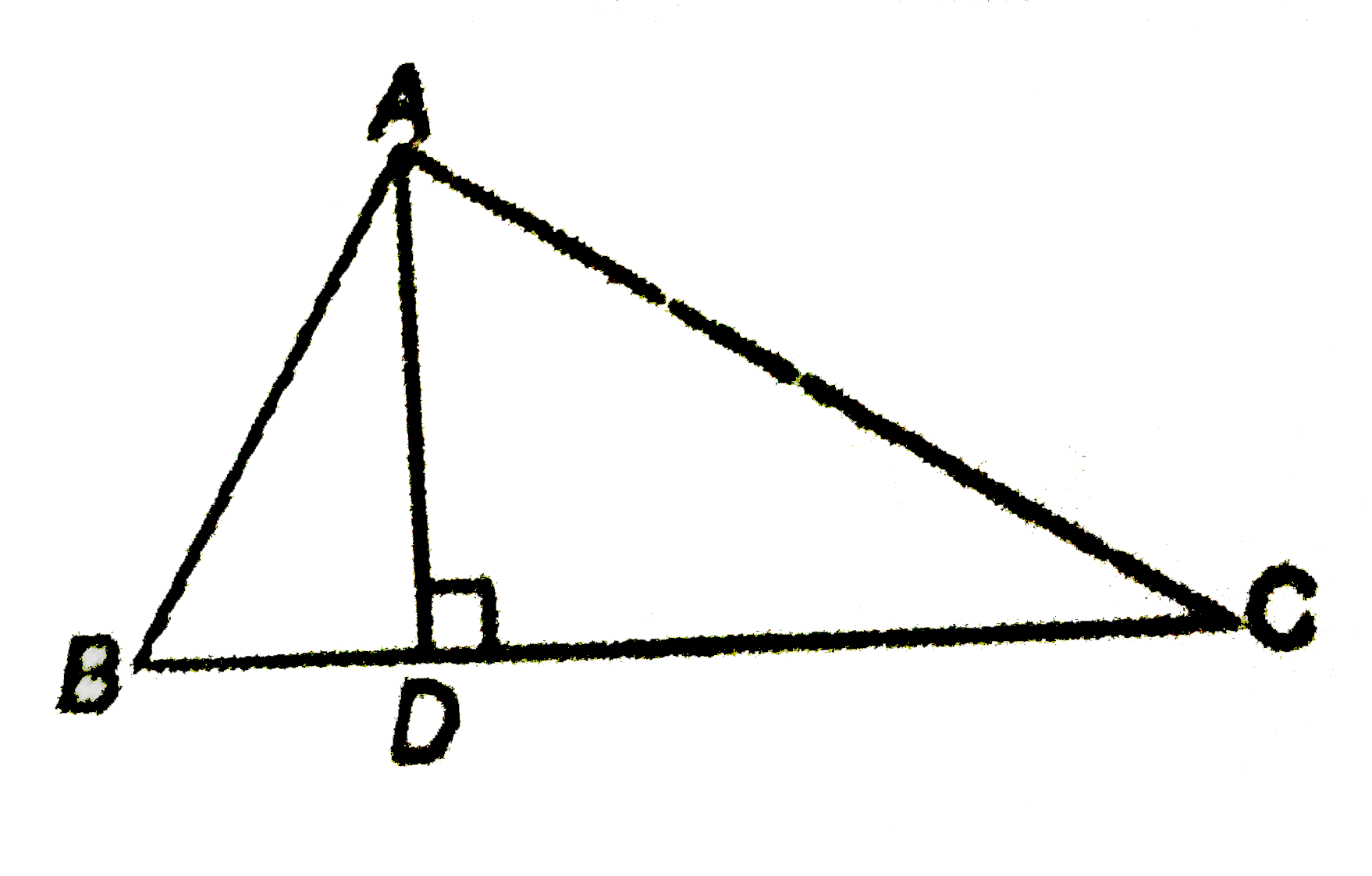
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIn ΔABC,∠B=∠C. Prove the perpendiculars from the mid-point of BC to AB and AC are equal.
View SolutionIn a rectangle ABCD, prove that : AC2+BD2=AB2+BC2+CD2+DA2.
View Solution
