A(1,−2)andB(2,5) are two points. The lines OA,OB are produced to CandD respectively, such that OC=2OAandOD=2OB. Find CD.
Step by step video & image solution for A(1, -2) and B(2, 5) are two points. The lines OA, OB are produced to C and D respectively, such that OC=2OA and OD=2OB. Find CD. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
On the xy plane where O is the origin, given points, A(1,0),B(0,1)andC(1,1). Let P,Q,andR be moving points on the line OA,OB,OC respectively such that ¯¯¯¯¯¯OP=45t¯¯¯¯¯¯¯¯¯(OA),¯¯¯¯¯¯OQ=60t¯¯¯¯¯¯¯¯¯(OB),¯¯¯¯¯¯OR=(1−t)¯¯¯¯¯¯¯¯¯(OC) with t>0. If the three points P,QandR are collinear then the value of t is equal to
A 1106
B 7187
C 1100
D none of theseView SolutionO is the origin and lines OA, OB and OC have direction cosines lr,mrandnr(r=1,2and3). If lines OA', OB' and OC' bisect angles BOC, COA and AOB, respectively, prove that planes AOA', BOB' and COC' pass through the line xl1+l2+l3=ym1+m2+m3=zn1+n2+n3.
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View SolutionTwo concentric shells of uniform density of mass M1 and M2 are situated. The forces experienced by a particle of mass m when palced at positions A,B and C respectively are given OA =p,OB = q and OC =r .
 .View Solution
.View SolutionA line through the origin intersects x=1,y=2andx+y=4, in A,BandC respectively,such that OA⋅OB⋅OC=8√2. Find the equation of the line.
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
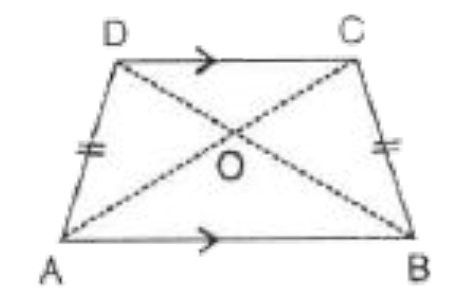
Prove that:
OA = OB and OC= ODView SolutionTwo particles 1 and 2 are allowed to descend on the two frictionless chord OA and OB of a vertical circle, at the same instant from point O. The ratio of the velocities of the particles 1 and 2 respectively, when they reach on the circumference will be (OB is the diameter).
View SolutionIn the figure, OA and OB are two uniformly charged wires, placed along x and y axis respectively. Find the unit vector in the direction of field at point (0,0,√3L).
 View Solution
View SolutionTwo fixed point AandB are taken on the two axes such that OA=a,OB=b, two variable points C,D are taken on the same axes respectively, find the locus of the point of intersection of ADandCB if : 1OC−1OD=1OA−1OB
View SolutionA and B are two points on the parabola y2=4ax with vertex O. if OA is perpendicular to OB and they have lengths r1 and r2 respectively, then the valye of r4/31r4/32r2/31+r2/32 is
View Solution

