In the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear
To determine which vectors are collinear in the rectangle ABCD, we will analyze the vectors associated with the sides of the rectangle.
1. Identify the Vectors:
In rectangle ABCD, we can define the vectors as follows:
- Let →A represent vector AB.
- Let →B represent vector BC.
- Let →C represent vector CD.
- Let →D represent vector DA.
2. Understand Collinearity:
Two vectors are said to be collinear if they lie along the same line or are parallel to each other. This means one vector can be expressed as a scalar multiple of the other.
3. Analyze the Vectors:
- In a rectangle, opposite sides are equal in length and parallel. Therefore:
- Vector →A (AB) is parallel to vector →C (CD).
- Vector →B (BC) is parallel to vector →D (DA).
4. Conclusion on Collinearity:
- Since →A and →C are parallel, we conclude that:
→A and →C are collinear.
- Similarly, since →B and →D are parallel, we conclude that:
→B and →D are collinear.
5. Final Statement:
Therefore, the pairs of collinear vectors in rectangle ABCD are:
- →A and →C
- →B and →D
In rectangle ABCD, we can define the vectors as follows:
- Let →A represent vector AB.
- Let →B represent vector BC.
- Let →C represent vector CD.
- Let →D represent vector DA.
Two vectors are said to be collinear if they lie along the same line or are parallel to each other. This means one vector can be expressed as a scalar multiple of the other.
- In a rectangle, opposite sides are equal in length and parallel. Therefore:
- Vector →A (AB) is parallel to vector →C (CD).
- Vector →B (BC) is parallel to vector →D (DA).
- Since →A and →C are parallel, we conclude that:
→A and →C are collinear.
- Similarly, since →B and →D are parallel, we conclude that:
→B and →D are collinear.
Therefore, the pairs of collinear vectors in rectangle ABCD are:
- →A and →C
- →B and →D
Similar Questions
In the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
View SolutionIn the adjoining figure find ∠x
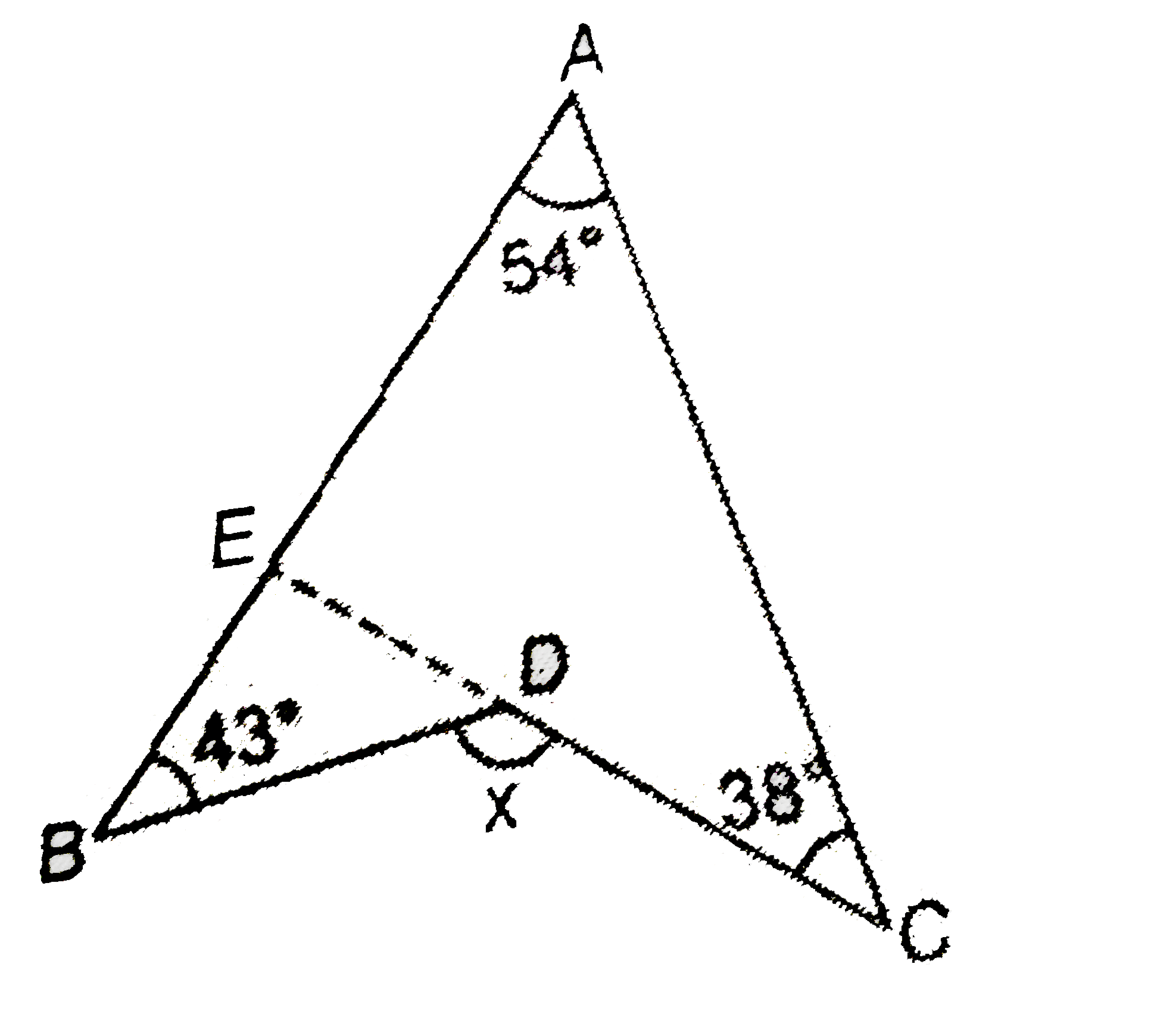
View SolutionIn the adjoining figure find ∠x
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, collinear
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Collinear but not equal
View SolutionIn the adjoining figure which of the vector are: collinear

View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
View Solutionin the adjoining figure find ∠F.
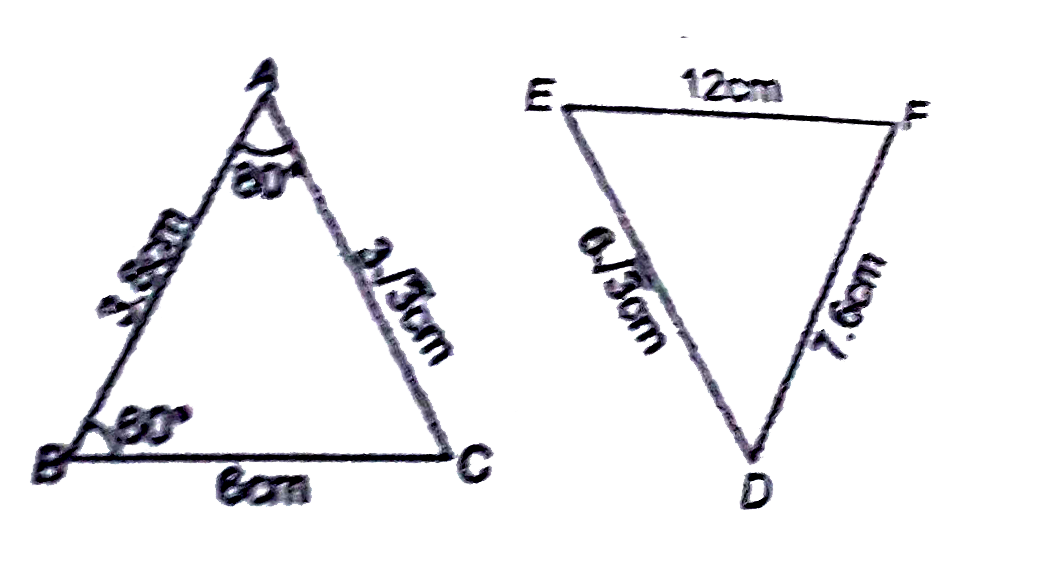
View Solution
