In the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
To determine which vectors are co-initial in the regular hexagon ABCDEF, we need to analyze the starting points of each vector. Co-initial vectors are those that originate from the same point. Let's go through the steps systematically.
1. Identify the Points of the Hexagon:
The vertices of the hexagon are labeled as A, B, C, D, E, and F.
2. List the Vectors:
Assume we have vectors represented as follows:
- →a starting from point A
- →b starting from point B
- →c starting from point C
- →d starting from point D
- →e starting from point E
- →f starting from point F
- →u,→v,→α,→β,→γ are other vectors associated with the points.
3. Check for Co-initial Vectors at Each Vertex:
- At Point A:
- Vectors →a,→β,→u start from point A.
- Thus, the first pair of co-initial vectors is →a,→β,→u.
- At Point B:
- Only vector →b starts from point B.
- No co-initial vectors here.
- At Point C:
- No vectors start from point C.
- No co-initial vectors here.
- At Point D:
- Vectors →d and →γ start from point D.
- Thus, the second pair of co-initial vectors is →d,→γ.
- At Point E:
- Only vector →e starts from point E.
- No co-initial vectors here.
- At Point F:
- Only vector →f starts from point F.
- No co-initial vectors here.
4. Conclusion:
The co-initial vectors identified are:
- Pair 1: →a,→β,→u (from point A)
- Pair 2: →d,→γ (from point D)
Final Answer:
The pairs of co-initial vectors are →a,→β,→u and →d,→γ.
The vertices of the hexagon are labeled as A, B, C, D, E, and F.
Assume we have vectors represented as follows:
- →a starting from point A
- →b starting from point B
- →c starting from point C
- →d starting from point D
- →e starting from point E
- →f starting from point F
- →u,→v,→α,→β,→γ are other vectors associated with the points.
- At Point A:
- Vectors →a,→β,→u start from point A.
- Thus, the first pair of co-initial vectors is →a,→β,→u.
- Only vector →b starts from point B.
- No co-initial vectors here.
- No vectors start from point C.
- No co-initial vectors here.
- Vectors →d and →γ start from point D.
- Thus, the second pair of co-initial vectors is →d,→γ.
- Only vector →e starts from point E.
- No co-initial vectors here.
- Only vector →f starts from point F.
- No co-initial vectors here.
The co-initial vectors identified are:
- Pair 1: →a,→β,→u (from point A)
- Pair 2: →d,→γ (from point D)
The pairs of co-initial vectors are →a,→β,→u and →d,→γ.
Similar Questions
Knowledge Check
In the figure shown, ABCDEF is a regular hexagon and AOF is an equilateral triangle. The perimeter of ΔAOF is 2a feet. What is the perimeter of the hexagon in feet?
 A2aB3aC4aD6a
A2aB3aC4aD6a
In the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
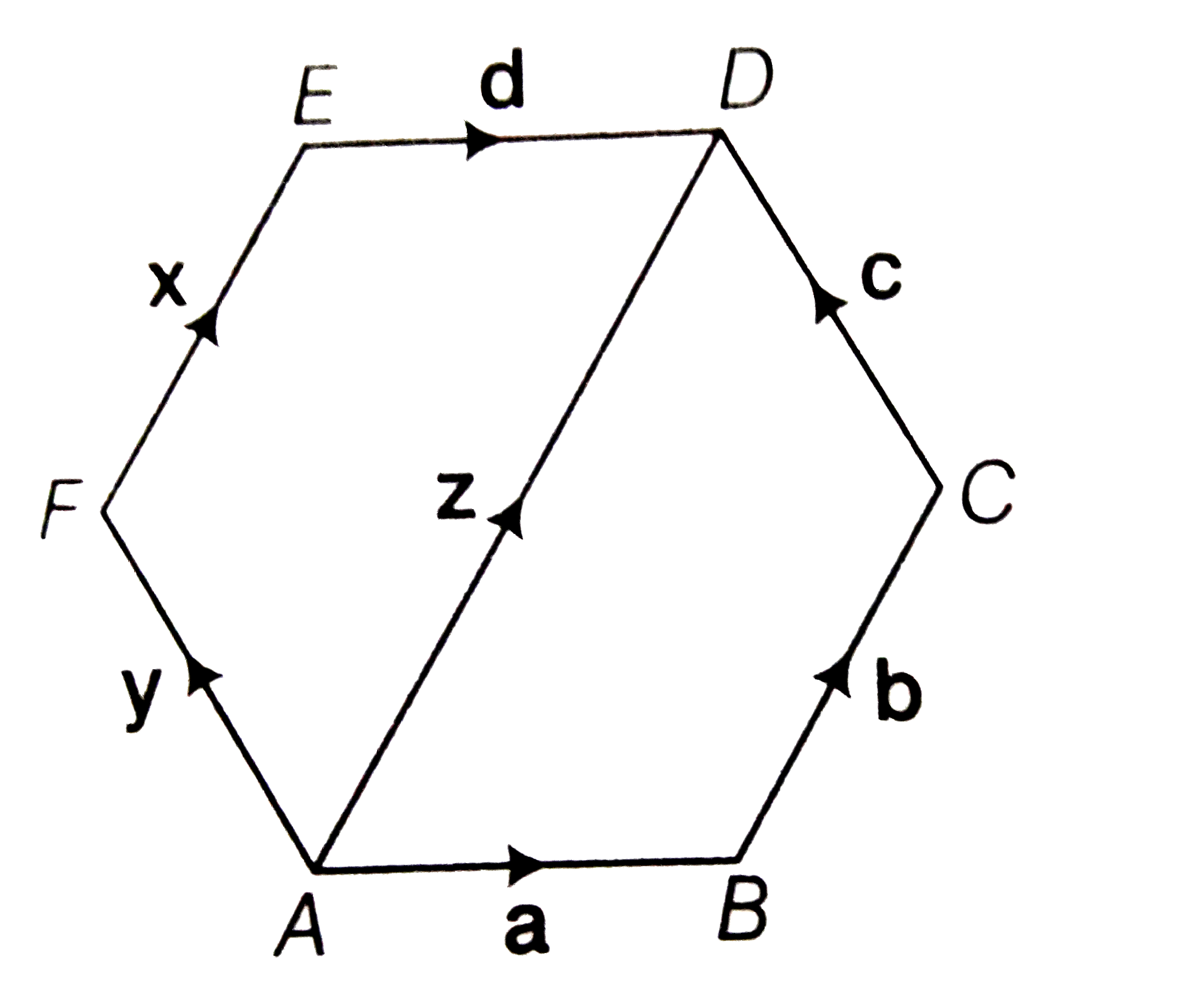
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure, ABCDEF is a regular hexagon. Prove that □ABDE,□ACDFand□AGDH are parallelograms.
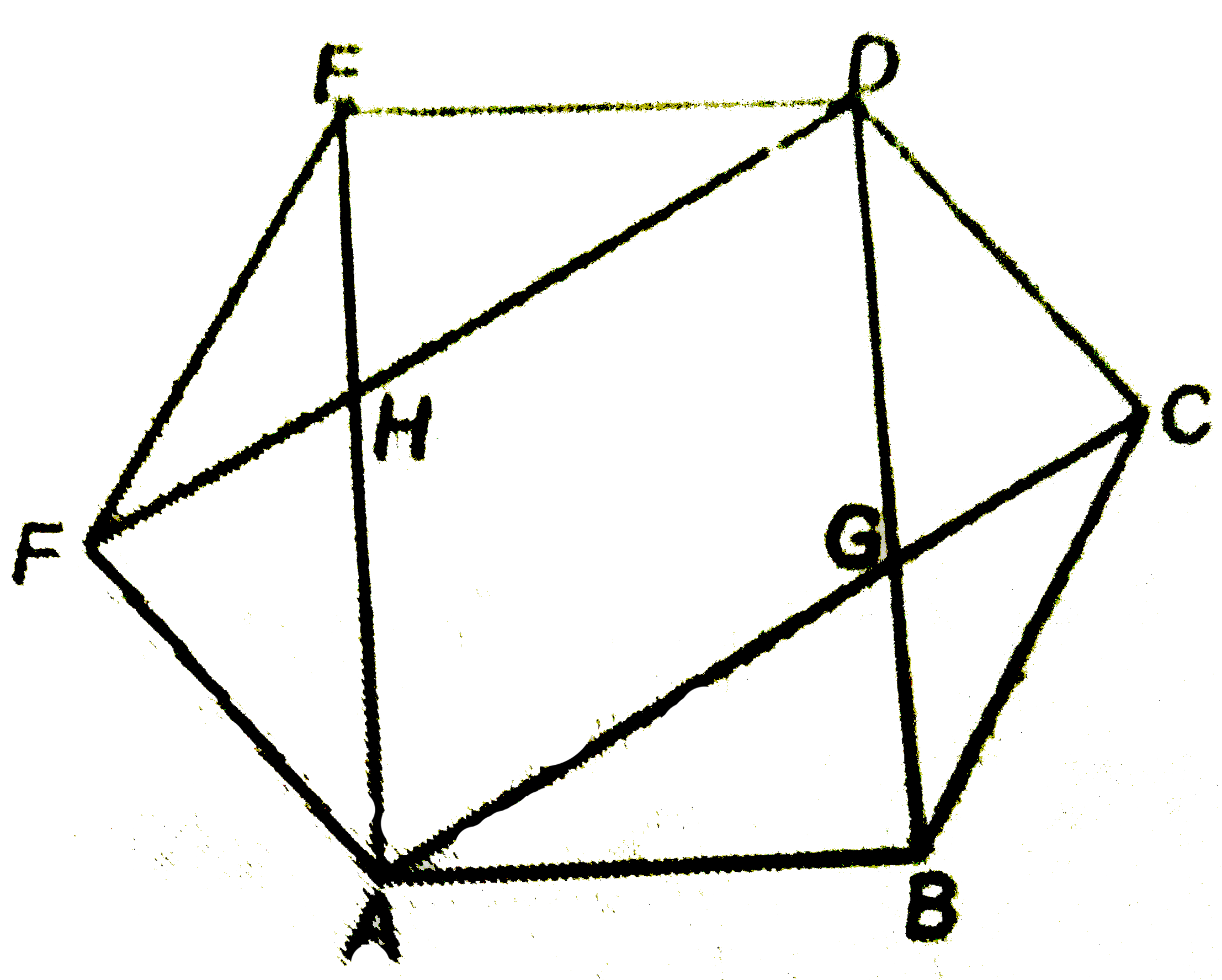
View Solution
