In the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
To determine which vectors are co-initial in the rectangle ABCD, we need to analyze the starting points of the vectors. Co-initial vectors are those that start from the same point.
1. Identify the Points of the Rectangle:
- The rectangle ABCD has four corners: A, B, C, and D.
2. Define the Vectors:
- Let’s assume the vectors are defined as follows:
- Vector A originates from point A.
- Vector B originates from point B.
- Vector C originates from point C.
- Vector D originates from point D.
3. Examine Point A:
- At point A, we have:
- Vector A starting from A.
- Vector C also starting from A.
- Since both vectors start from the same point, A and C are co-initial.
4. Examine Point B:
- At point B, we have:
- Vector B starting from B.
- Vector D ending at B.
- Since vector D does not start from B, vectors B and D are not co-initial.
5. Examine Point C:
- At point C, we have:
- Vector C ending at C.
- Vector B starting from C.
- Since vector C ends at C and vector B starts from C, they are not co-initial.
6. Examine Point D:
- At point D, we have:
- Vector D starting from D.
- Vector A ending at D.
- Since vector A does not start from D, vectors A and D are not co-initial.
7. Conclusion:
- The only pair of co-initial vectors identified is A and C.
Final Answer:
The vectors that are co-initial are A and C.
- The rectangle ABCD has four corners: A, B, C, and D.
- Let’s assume the vectors are defined as follows:
- Vector A originates from point A.
- Vector B originates from point B.
- Vector C originates from point C.
- Vector D originates from point D.
- At point A, we have:
- Vector A starting from A.
- Vector C also starting from A.
- Since both vectors start from the same point, A and C are co-initial.
- At point B, we have:
- Vector B starting from B.
- Vector D ending at B.
- Since vector D does not start from B, vectors B and D are not co-initial.
- At point C, we have:
- Vector C ending at C.
- Vector B starting from C.
- Since vector C ends at C and vector B starts from C, they are not co-initial.
- At point D, we have:
- Vector D starting from D.
- Vector A ending at D.
- Since vector A does not start from D, vectors A and D are not co-initial.
- The only pair of co-initial vectors identified is A and C.
The vectors that are co-initial are A and C.
Similar Questions
In the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure find ∠x
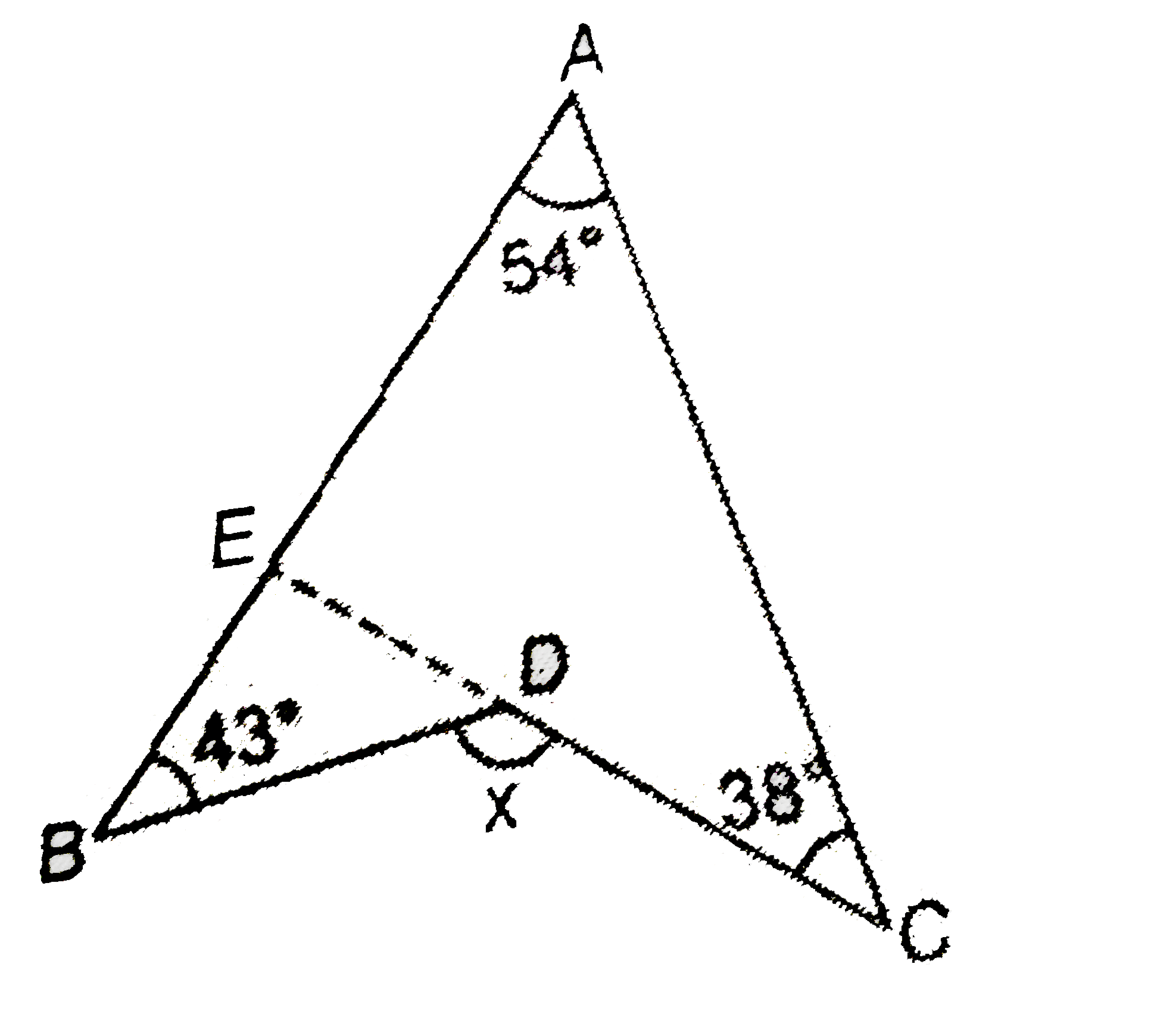
View SolutionIn the adjoining figure find ∠x
View SolutionIn the adjoining figure AB||CD, find x and y

View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, collinear
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
View SolutionIn the adjoining figure which of the vector are: cointial

View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View Solution
