Sketch the region of relation [x]+[y]=5,x,y≥0, where [⋅] denots the greatest integer function. Solution in Tamil
[x]+[y]=5
For 0≤x<1,0+[y]=5or[y]=5or5≤x<6
Thus, the points lie in the region stisfying 0≤x<1and5≤x<6 as shown in the following figure.
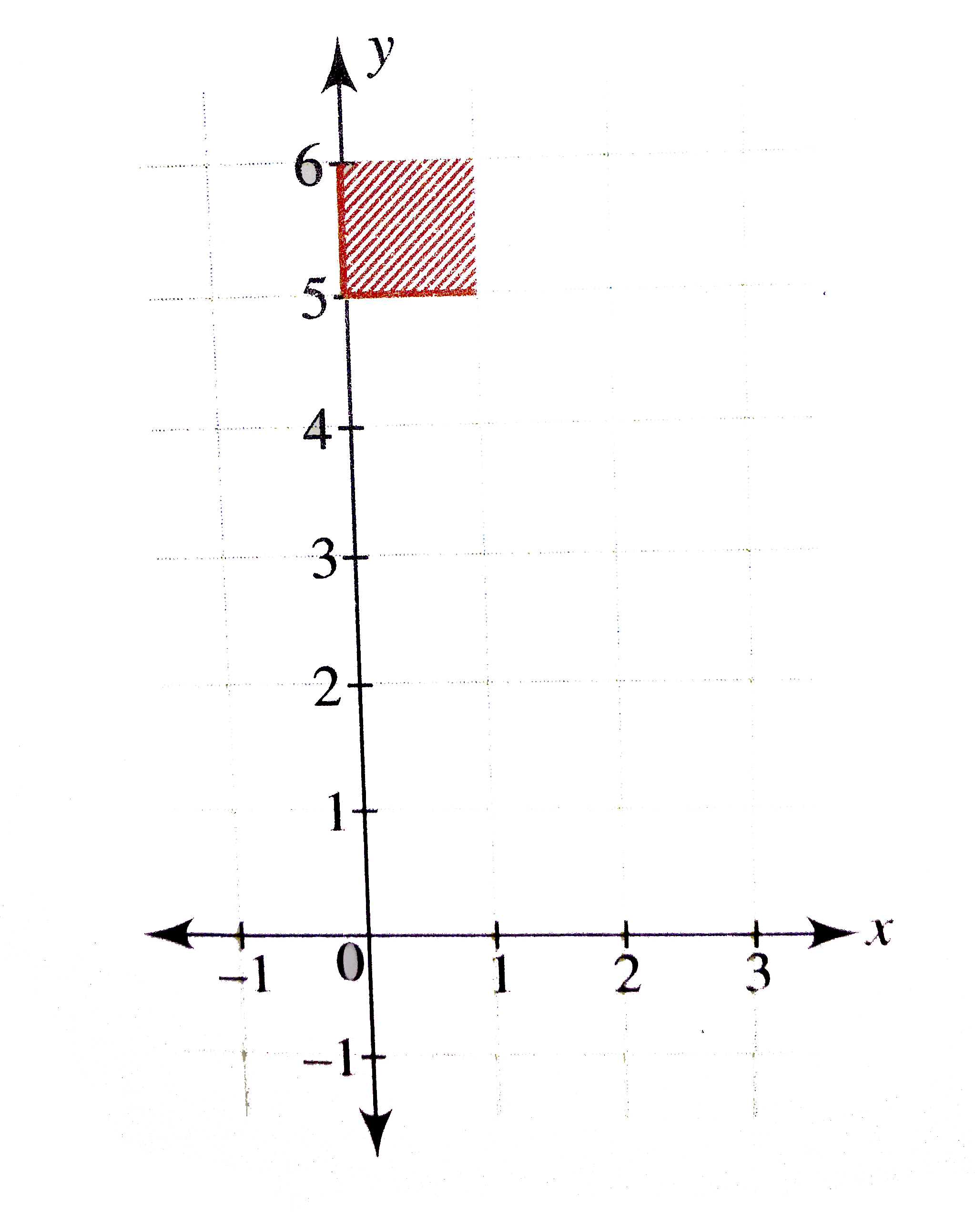
Thus, we have the following values of x and the corresponding values of y.
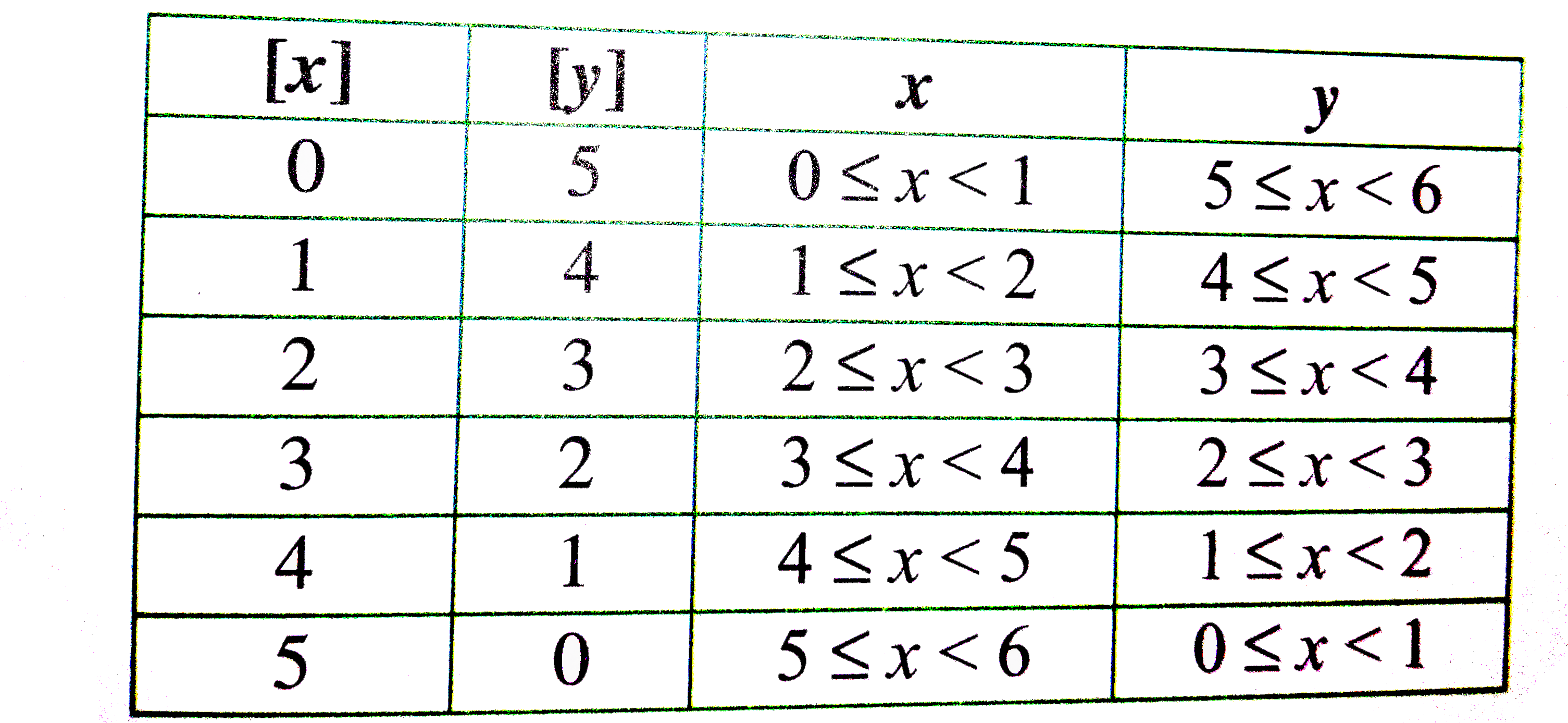
The region satisfying the above conditions is as shown in the following figure.
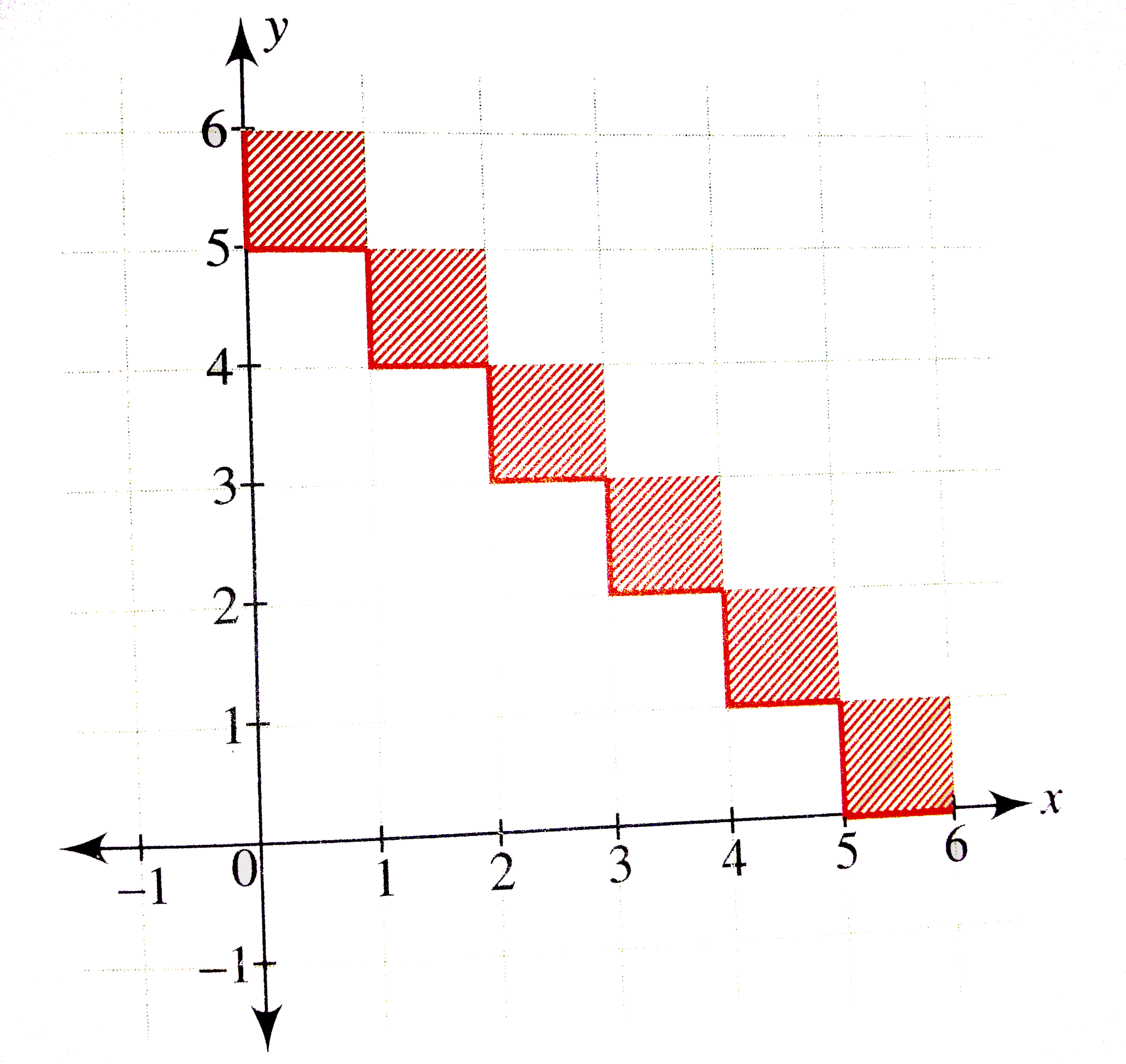
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionIf x>=0 and y>=0 ,then the area bounded by the graph of [x]+[y]=2 is (where [] denotes greatest integer function)
View SolutionSketch the region of relation [x]+[y]=5,x,y≥0, where [⋅] denots the greatest integer function.
View SolutionDraw the region of relation [x][y]=6,x,y≥0. Here [⋅] denotes the greatest integer function.
View SolutionSketch the curves
(i)y=√x−[x]
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(ii) y=[x]+√x−[x]
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionSketch the region of relation [x]+[y]=5,x,y≥0, where [⋅] denots the greatest integer function.
View SolutionDraw the region of relation [x][y]=6,x,y≥0. Here [⋅] denotes the greatest integer function.
View SolutionSketch the curves
(i)y=√x−[x]
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(ii) y=[x]+√x−[x]
(where [.] denotes the greatest integer function).
View SolutionSketch the curves
(iii) y=∣∣[x]+√x−[x]∣∣
(where [.] denotes the greatest integer function).
(where [.] denotes the greatest integer function).
View Solution
