Let z1 and z2 be complex numbers such that z21−4z2=16+20i and the roots α and β of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7.
The maximum value of |m| is
14
2√7
7+√41
2√6−4
The correct Answer is:C
(c) We have α+β=−z1 and αβ=z2+m
(α−β)2=(α+β)2−4αβ
=z1(^(2)−4z1−4m
=16+20i−4m
Since|α−β|=2√7, we have |4+5i−m|=7……(i)
Therfore, m lies on a circle having centre at (4,5) and radius =7.
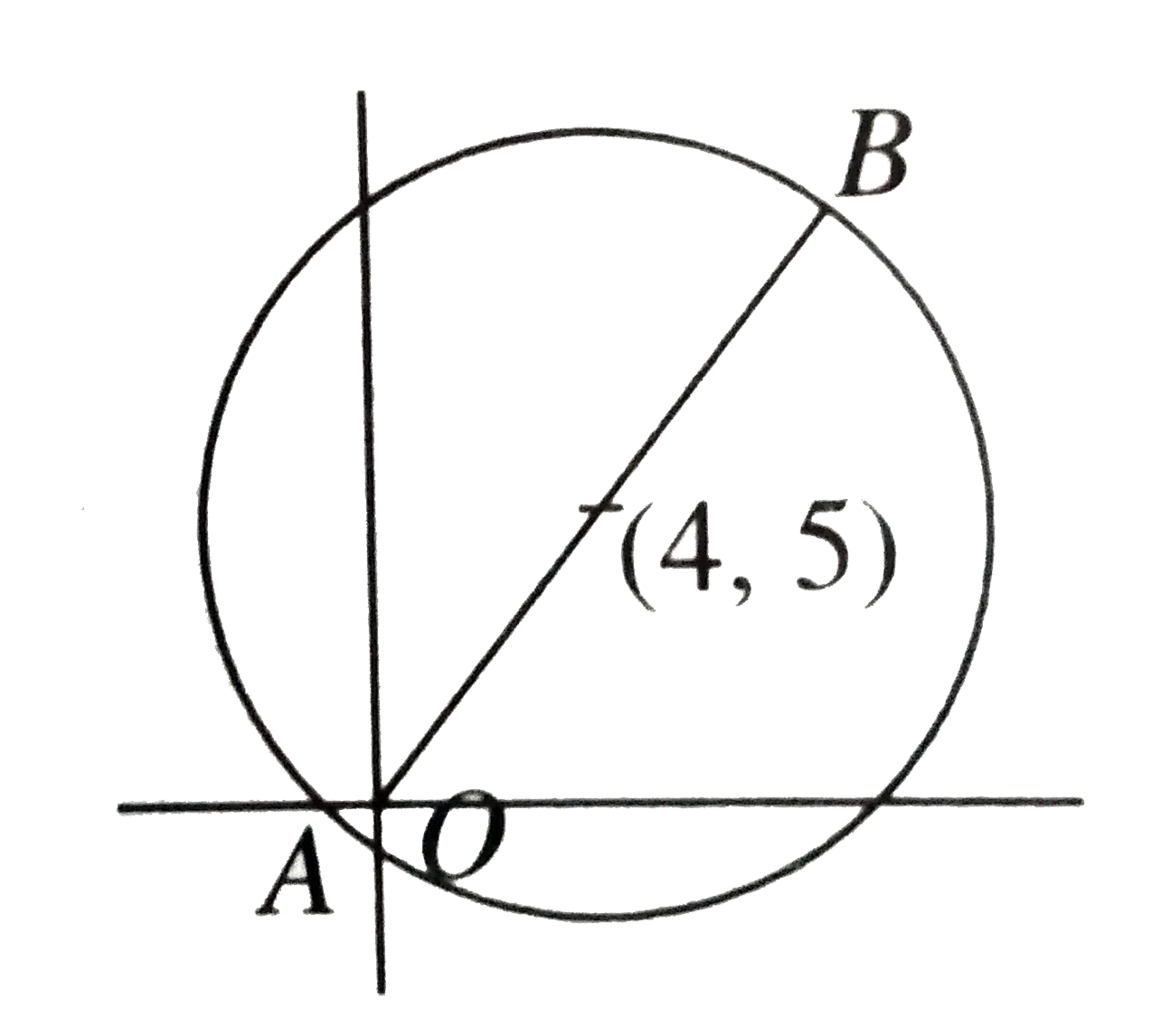
|m|max=OB=7+√41
Maximum argument of m is π which occurs at point A,
Let m=x+iy
For point A, m=x
So from (i), |4+5i−x|=7
or (x−4)2=24
⇒x−4=±2√6
⇒x=4±2√6
For point A, x=2√6−4
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Examples
125 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise 3.1
4 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
Let z1 and z2 be complex numbers such that z21−4z2=16+20i and the roots α and β of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7. The value of |m|,
View SolutionLet z1andz2 be complex numbers such that z21−4z2=16+20i and the roots αandβ of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7.
The minimum value of |m| is
View Solution
Knowledge Check
Let z1andz2 be complex numbers such that z21−4z2=16+20i and the roots αandβ of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7.
The minimum value of |m| isA7B28−√41C√41D7−√41Let z1 and z2 be complex numbers such that z21−4z2=16+20i and the roots α and β of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7. The value of |m|, when are(m) is maximum
A7B28−√41C√41D2√6−4Let z1 and z2 be complex numbers such that z21−4z2=16+20i and the roots α and β of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7.
The locus of the complex number m is a curveAstraight lineBcircleCellipseDhyperbola
Let z1 and z2 be complex numbers such that z21−4z2=16+20i and the roots α and β of x2+z1x+z2+m=0 for some complex number m satisfies |α−β|=2√7.
The locus of the complex number m is a curve
View SolutionLet z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,
View SolutionLet z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,
View SolutionLet z1=6+i&z2=4−3i Let z be a complex number such that arg(z−z1z−z2)=π2 then z satisfies
View SolutionLet z1,z2 be two complex numbers such that |z1+z2|=|z1|+|z2|. Then,
View Solution
