A person walks 2√2 units away from origin in south west direction (S45∘W) to reach A, then walks √2 units in south east direction (S45∘E) to reach B. From B he travel is 4 units horizontally towards east to reach C. Then he travels along a circular path with centre at origin through an angle of 2π/3 in anti-clockwise direction to reach his destination D.
Position of D in argand plane is (w is an imaginary cube root of unity)
(3+i)ω
−(1+i)ω2
3(1−i)ω
(1−3i)ω
The correct Answer is:C
(c)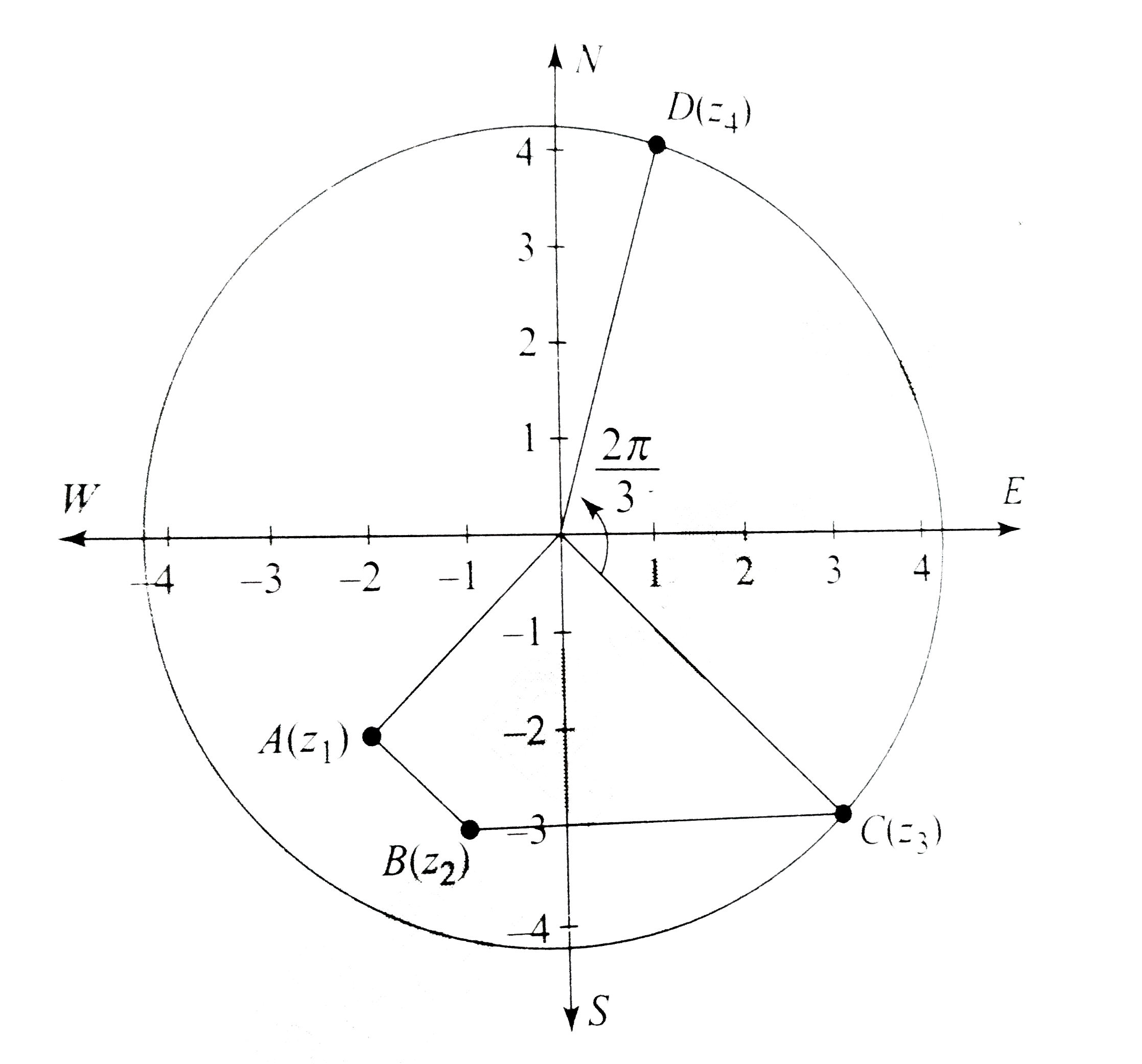 
Z1=2√2e−i3π/4=−2−2i
Z2−(−2−2i)O−(−2−2i)=12×e−iπ/2 (rotation at A)
⇒Z2=−(1+i)(2−i)=−1−3i
∴Z3=3−3i
Z4−03−3i−0=ei2π/3⇒Z4=3(1−i)ω(rotation at O)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Examples125videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Exercise 3.14videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
A man walks a distance of 3 units from the origin towards north-east to reach position A. from there he walks a distance of 4 units towards North west to reach position P. Then position of P in argand plane is
View Solution'A' starts from origin and travels 1 unit distance along positive x-axis to reach P. From there he travels 2 unit parallel to y- axis to reach Q . Then the travels 3 unit distance parallel to y=x and away from origin to reach "R" .Then he rotates about O in anticlockwise direction so as to reach y-axis at S .If the co-ordinates of S are (0,S) then √2(S2−14) would be equal to
View Solution
Knowledge Check
- Question 1 - Select One
A person walks 2√2 units away from origin in south west direction (S45∘W) to reach A, then walks √2 units in south east direction (S45∘E) to reach B. From B he travel is 4 units horizontally towards east to reach C. Then he travels along a circular path with centre at origin through an angle of 2π/3 in anti-clockwise direction to reach his destination D.
Let the complex number Z represents C in argand plane. then arg(Z)=A−π6Bπ4C−π4Dπ3 - Question 2 - Select One
A man walks a distance of 3 units from the origin towards the North-East (N450E) direction.From there, he walks a distance of 4 units towards the North-West (N450W) direction to reach a point P. Then, the position of P in the Argand plane is 3eiπ4+4i (b) (3−4i)eiπ4 (4+3i)eiπ4 (d) (3+4i)eiπ4
A3eiπ/4+4iB(3−4i)eiπ/4C(4+3i)eiπ/4D(3+4i)eiπ/4 - Question 3 - Select One
Nimisha started walking towards south to reach her school which is 5 km away. From there she turns 180∘ in clockwise and then 45∘ in anticlockwise direction. Which direction is she facing now from her school ?
ASouthBNorthCSouth-eastDNorth-west
Dipak walks from point P 15 m to the east to reach point Q. then he takes right turn and walks for 20 m to reach point R. now he takes a left turn and walks for 15m to reach point S. now he takes a left turn and walks for 10 m to reach point T. then he takes a right turn and walks for 5 m to reach point V. now ke takes a left turn and walks for 10m to reach point W.
Point R is in which direction with respect to point T?View SolutionA particle starts from a point z0=1+i where i=√−1. lt moves horizontally away from origin by 2 units and then vertically away from origin by 3 units to reach a point z1, From z1 particle moves √5 units in the direction of 2ˆi+3ˆj and then it moves through à n angle of cosec−12 in anticlockwise direction of a circle with centre at origin to reach a point z2. The arg z1 is given by
View SolutionIn the Cartesian plane, a man starts at origin and walks a distance of 3 units of the north-east direction and reaches a point P. from P, he walks a distance of 4 units in the north-west direction to reach a point Q. construct the parallelogram OPQR with OP and PQ as adjacent sides. let M be the mid-point of PQ.
View SolutionA particle P starts from the point z0=1+2i, where i=√−1 . It moves first horizontally away from origin by 5 units and then vertically away from origin by 3 units to reach a point z1. From z1 the particle moves √2 units in the direction of the vector ˆi+ˆj and then it moves through an angle π2 in anticlockwise direction on a circle with centre at origin, to reach a point z2. The point z2 is given by 6+7i (b) −7+6i 7+6i (d) −6+7i
View SolutionAnand travels 10 kms from his home to the east to reach his school Then he travels 5 kms to the south to reach his father's shop, after school. He then travels 10 kms to the west to help his uncle. How far and in which direction is he from his home?
View Solution