Draw the graph of y=loge(x3−x)Solution in Tamil
Video Solution
Text Solution
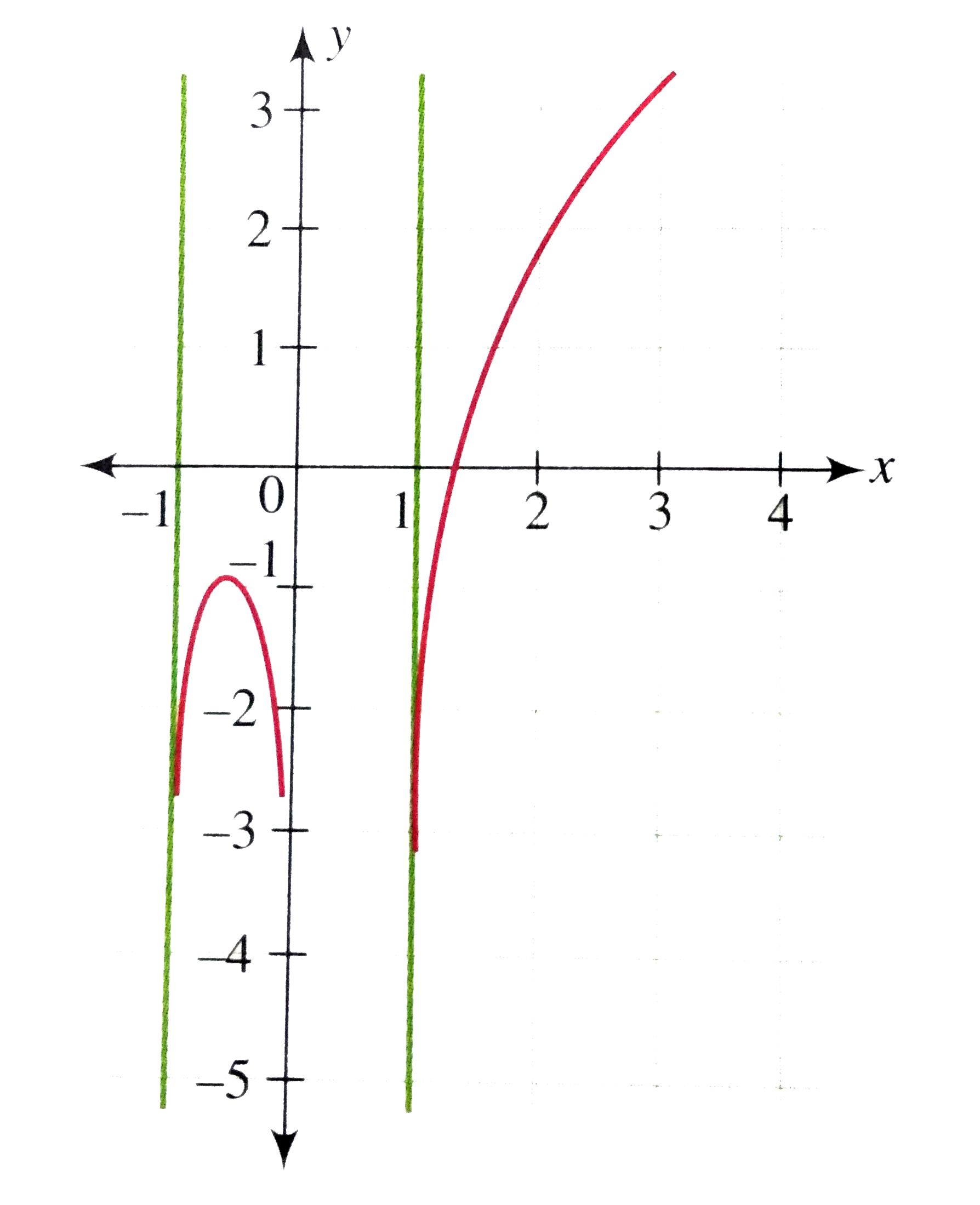
y=f(x)=loge(x3−x)
Here the function is defined if x3−x≥0
or x(x−1)(x+1)≥0
or x∈(−1,0)∪(1,∞)
limx→1+loge(x3−x)=loge0+=−∞
limx→0−logex(x2−1)=loge0+=−∞
logx→−1+ex(x2−1)=loge0+=−∞
For x>1,x3−x increases, so loge(x3−x) increases till infinity.
Also for f′(x)=3x2−1x3−1=0,x=−1√3 [as domain is (−1,0)∪(1,∞)]
Clearly, x=−1√3 is the point of maxima.
The graph of the function is as shown in the following figure.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Draw the graph of y=sin2x−cosx
02:01View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
02:54View SolutionSolve: (x+2)3=2x(x2−1)
02:00View SolutionDraw the graph of y=−logex.
View SolutionDraw the graph of y=|loge(x+3)|.
03:35View SolutionDraw the graph of y=|loge|x||.
02:50View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
01:47View SolutionDraw the graph of y=loge(x3−x)
05:39View SolutionDraw the graph of y=(logex)2
04:38View SolutionDraw the graph of y=|loge(x+3)|.
01:58View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
03:00View SolutionDraw the graph of y=loge(x3−x)
03:55View SolutionDraw the graph of y=-log_(e)x .
03:03View SolutionDraw the graph of y=|log_(e)(x+3)| .
01:48View SolutionDraw the graph of y=1/(log_(e)x)
03:19View Solution

