The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________Solution in Tamil
The correct Answer is:4
f(x)=12x2+6ax+3≥0∀x∈R
or 36a2−144≤0
or a∈[−2,2]
Thus number of nonzero integral values of a is 4
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - JEE Main Previous Year10videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - JEE Advanced Previous Year17videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type12videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank13videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Given P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1),then∈the∫erval[-1,1]
02:43View SolutionThe function f:[0,3]−−−→1,29, defined by f(x)=2x3−15x2+36x+1, is one-one and onto onto but not one-one one-one but not onto neither one-one nor onto
02:35View SolutionLet f be a function f:N→N be defined by f(x)=5x−3, Find the image of 3,4,5.
03:16View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
02:11View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?03:08View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
06:08View SolutionThe interval in which the function y=f(x)=(x-1)/(x^(2)-3x+3) transforms the real line is
09:40View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
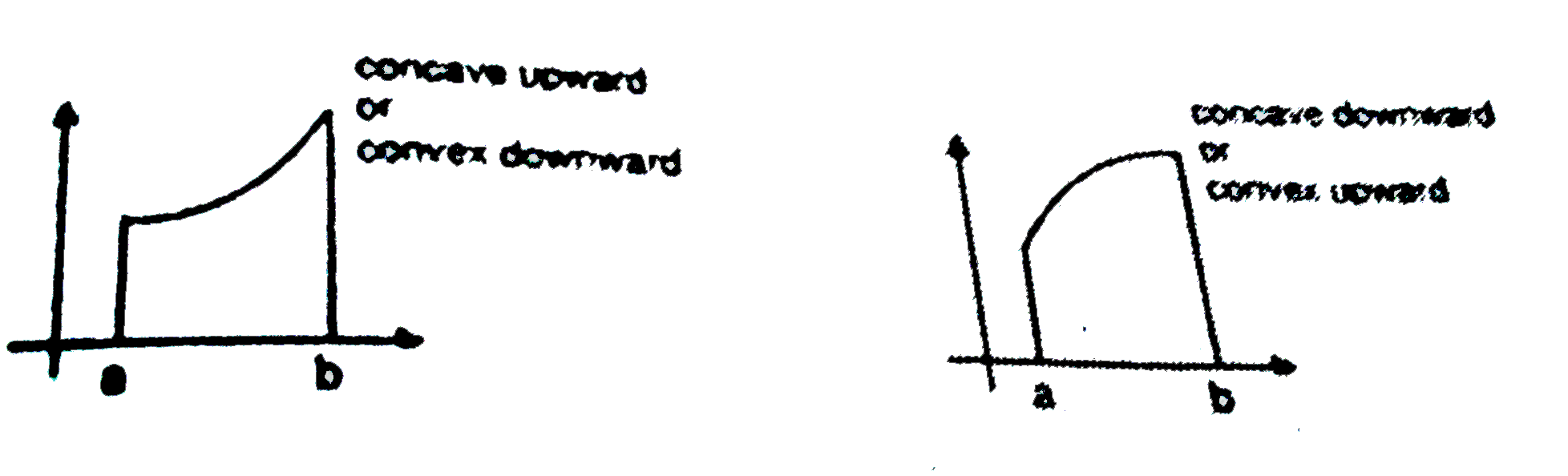
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :09:27View SolutionIf graph of the function f(x) =3x4+2x3+ax2−x+2 is concave upward for all real x, then find values of a,
02:49View SolutionStatement I :If f(x) is increasing function with upward concavity, then concavity of f−1(x) is also upwards.
Statement II : If f(x) is decreasing function with upwards concavity, then concavity of f−1(x) is alo upwards.02:39View SolutionThe function f(x)=2ax3+3x2+6(a−1)x+1 is decreasing for all real values of x .Then the greatest integral value of a is
03:07View SolutionThe function f(x)=2ax3+3x2+6(a−1)x+1 is decreasing for all real values of x .Then the greatest integral value of a is
05:06View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
02:50View SolutionIf graph of the function f(x) =3x4+2x3+ax2−x+2 is concave upward for all real x, then find values of a,
05:24View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
04:13View SolutionStatement I :If f(x) is increasing function with upward concavity, then concavity of f−1(x) is also upwards.
Statement II : If f(x) is decreasing function with upwards concavity, then concavity of f−1(x) is alo upwards.02:55View Solution

