The variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:Solution in Punjabi
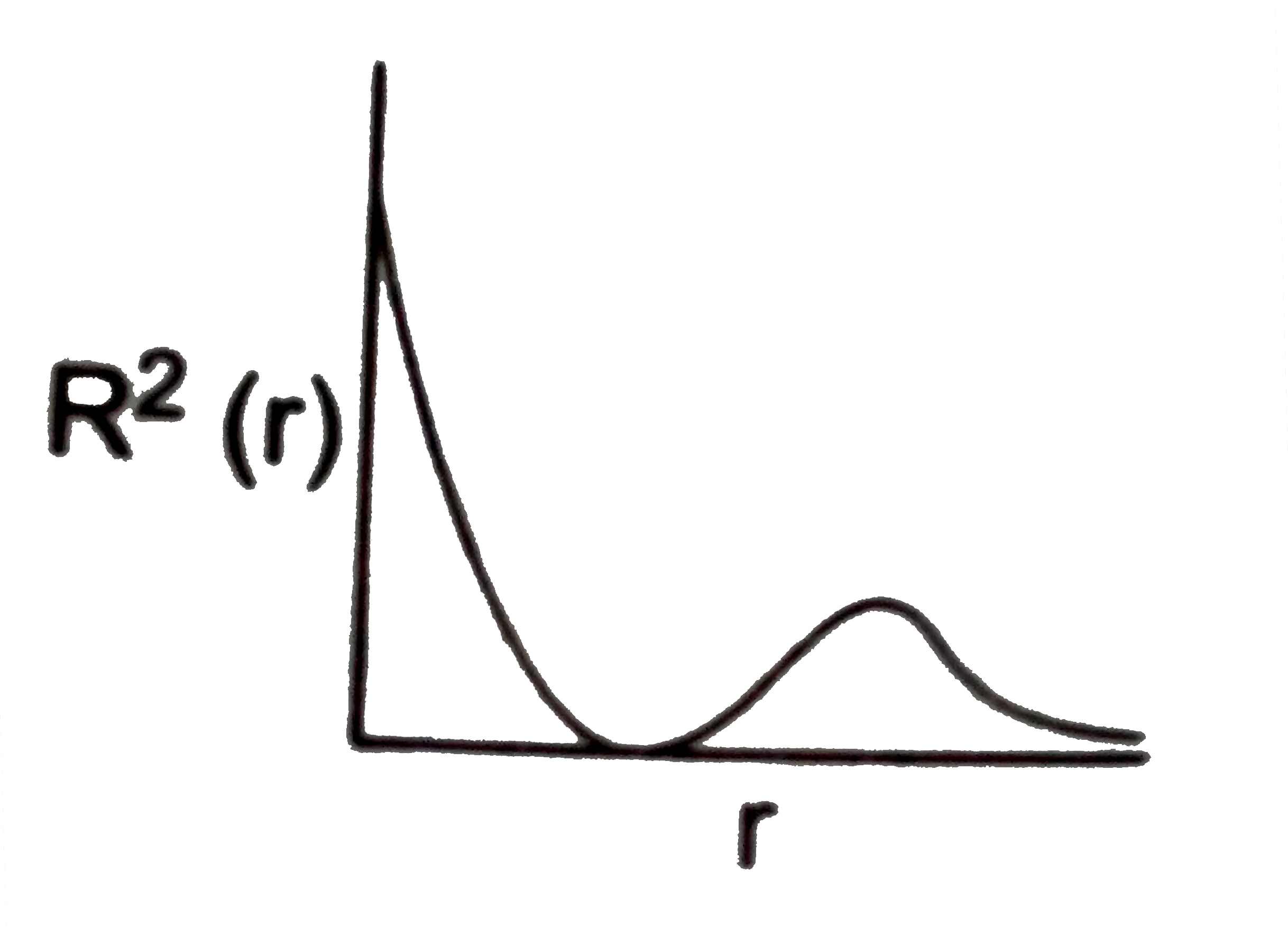
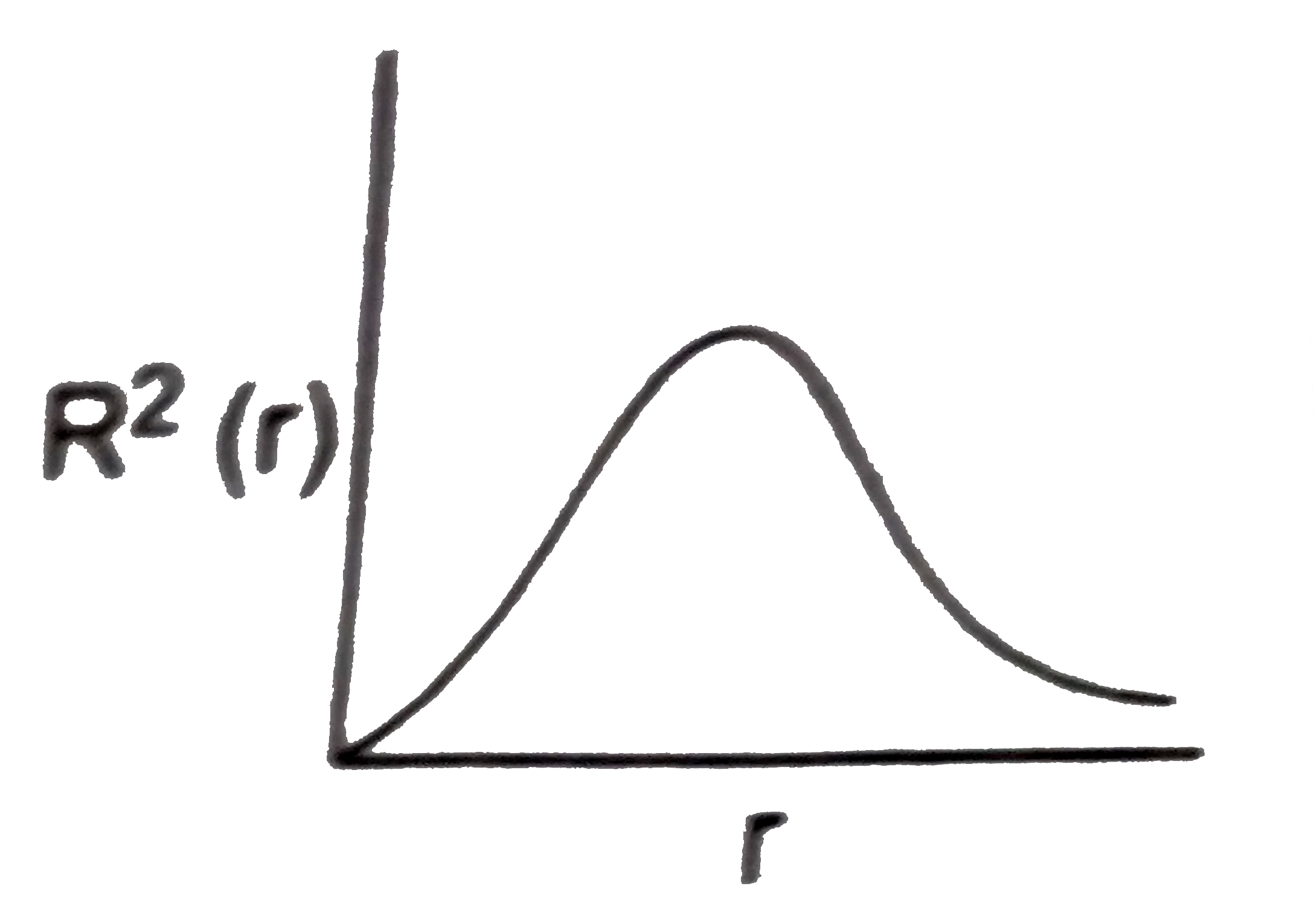
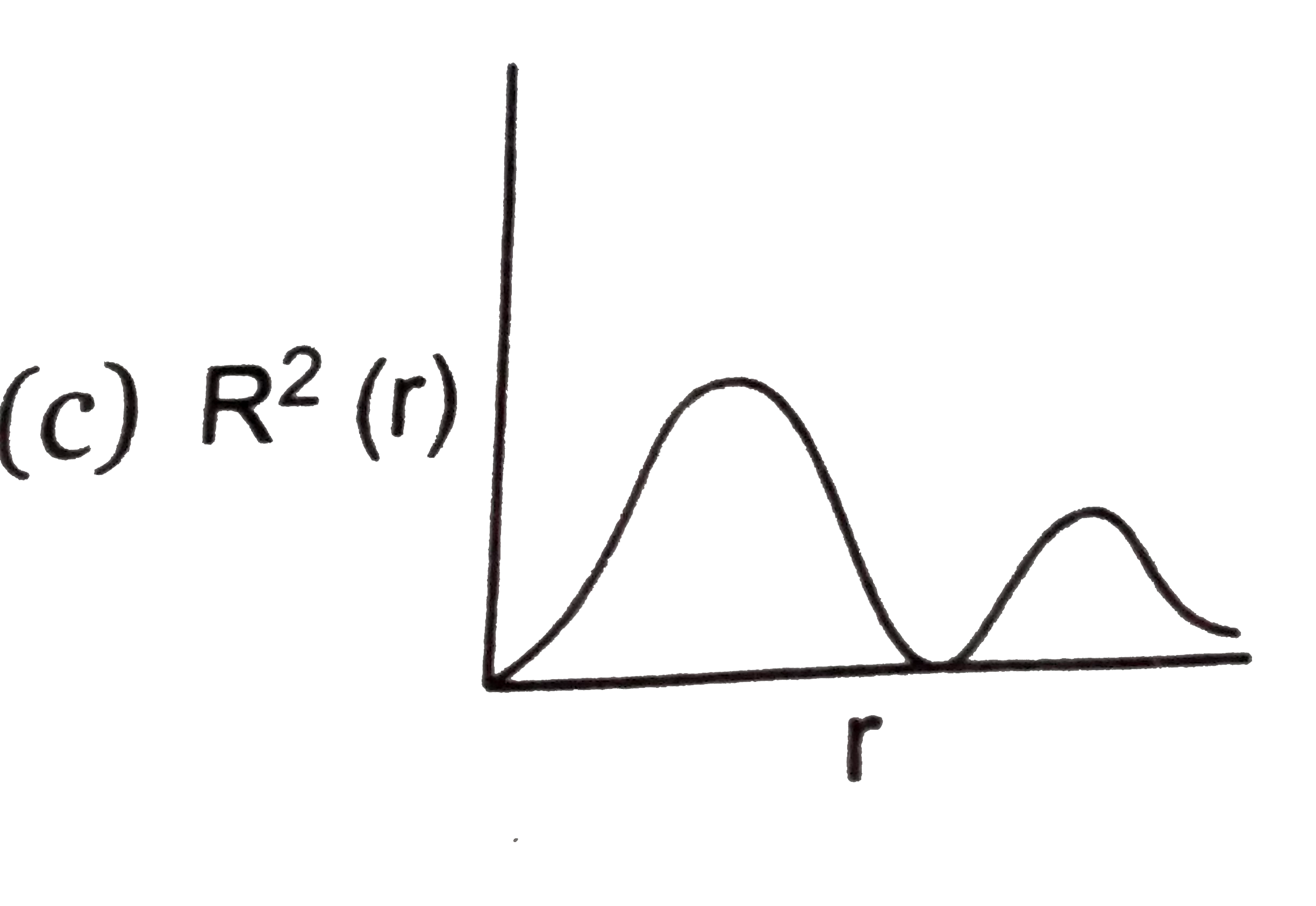
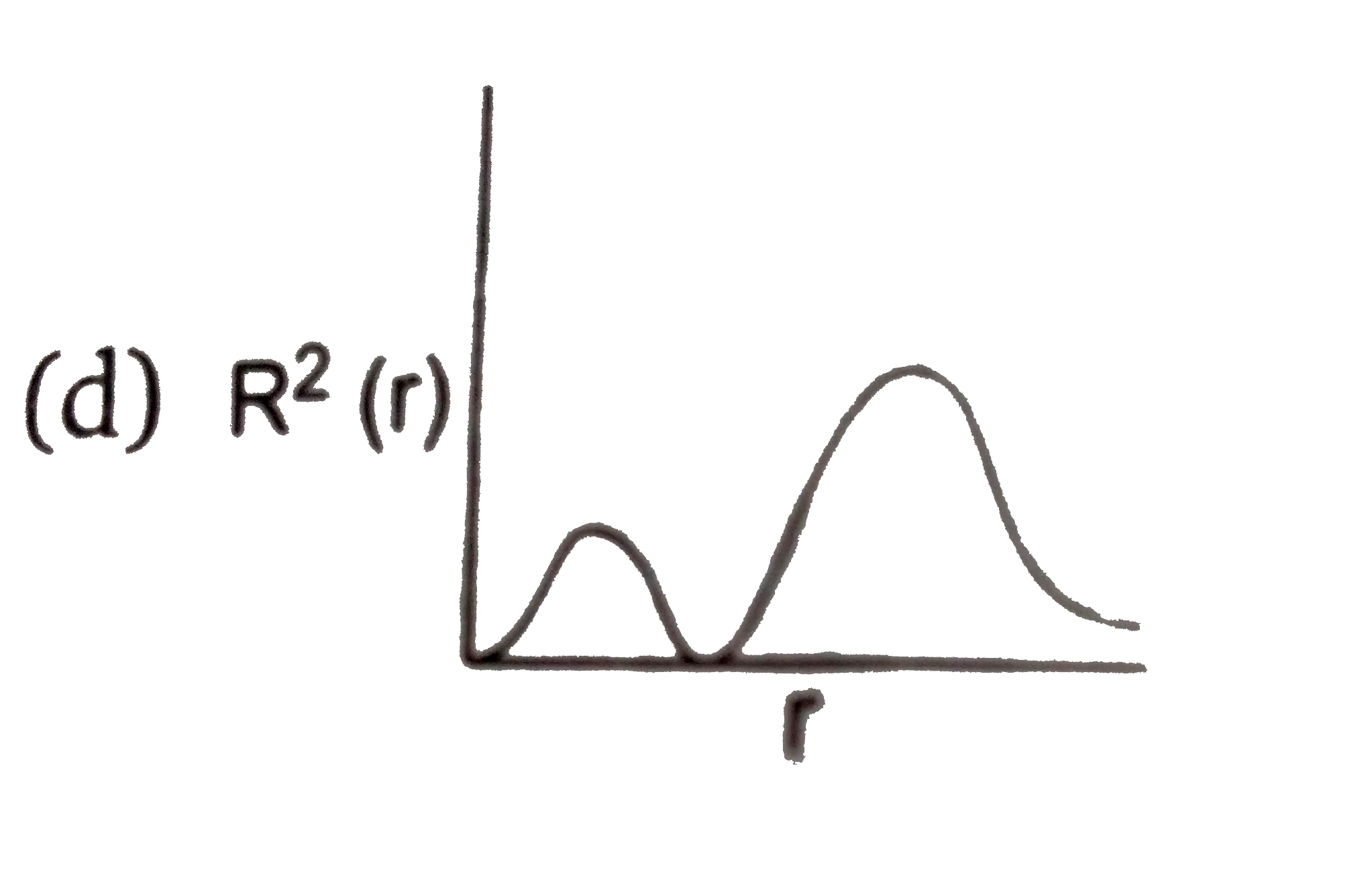
Step by step video & image solution for The variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which hybrid orbital is used by carbon atoms in the following molecules? CH3-CH3
View SolutionA small piece of mass m moves in such a way the P.E. =−12mkr2. Where k is a constant and r is the distance of the particle from origin. Assuming Bohr's model of quantization of angular momentum and circular orbit, r is directly proportional to :
View SolutionCalculate ΔrG for the reaction at 27∘C
H2(g)+2Ag+(aq)⇔2Ag(s)+2H+(aq)
Given : PH2=0.5 bar, [Ag+]=10−5M,
[H+]=10−3M,ΔrG∘[Ag+(aq)]=77.1kJ/mol
View SolutionOPERATOR FORM SCHRODINGER WAVE EQUATION,PLOT OF RADIAL WAVE FUNCTION 'R',PLOT OF RADIAL PROBABILITY DENSITY 'R^2
View SolutionFor which of the following orbitals is the radial probaility density R^(2) the maximum at the nucleus and descrease sharply as the distance form the nucleus increases?
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionR(r) is the radial part of the wave function and r is the distance of electron from the nucleus.
View SolutionWhich of the following is correct graph between Probability density sπ2(r) vs radial distance of electron (r) form nucleus for 3 s ?
View SolutionAssertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical Reason. Probability density is Psi^(2) whereas radial probability function represents probability of finding the electron in a shell of thickness dr .
View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r )=J_(0)(1-(r )/(R )) . The total current in the radial regon r = 0 to r=(R )/(4) will be :
View SolutionIf P(r) is the radial probability density for a hydrogen atom then the probability that the separation of the electron and proton is between r and r+ dr is
View SolutionThe variation of radial probability density R^2 (r) as a function of distance r of the electron from the nucleus for 3p orbital: (A)(a) (b) (b) (c) (d)
View SolutionFor 1s orbital Hydrogen atom radial wave function is given as: R(r) =1/(sqrtpi) ((1)/(a_0))^(3//2) e^(-r//a_0) (where a_0 = 0.529 A^@ ) .The ratio of radial probability density of finding electron at r = a_0 to the radial probability density of finding electron at the nucleus is given as (x.e^(-y)) . Calculate the value of (x + y).
View SolutionThe radial probability is the probability of finding electron in a small spherical shell around the nucleus at a particular distance r. Hence radial probability is
View SolutionRepresent graphically, the variation of probability density (ψ2_(r)) as a function of distance (r ) of the electron from the nucleus for 1s and 2s orbitals.
View Solution
