State whether the statements are true (T) or (F) false.
A quadrilateral can have all four angles as obtuse.
To determine whether the statement "A quadrilateral can have all four angles as obtuse" is true or false, we can follow these steps:
1. Understand the Definition of a Quadrilateral:
A quadrilateral is a polygon with four sides and four angles.
2. Know the Sum of Angles in a Quadrilateral:
The sum of the internal angles of any quadrilateral is always 360 degrees. This can be derived from the fact that a quadrilateral can be divided into two triangles, each having a sum of angles equal to 180 degrees. Therefore, 180+180=360 degrees.
3. Define Obtuse Angles:
An obtuse angle is an angle that is greater than 90 degrees but less than 180 degrees.
4. Set Up the Equation for All Obtuse Angles:
If we assume that all four angles of the quadrilateral are obtuse, we can denote them as:
- Angle A > 90 degrees
- Angle B > 90 degrees
- Angle C > 90 degrees
- Angle D > 90 degrees
5. Calculate the Minimum Sum of the Angles:
If each angle is greater than 90 degrees, we can express this mathematically:
Angle A+Angle B+Angle C+Angle D>90+90+90+90=360 degrees
6. Conclusion:
Since the sum of the angles exceeds 360 degrees when all angles are obtuse, it contradicts the fundamental property of quadrilaterals where the sum must equal 360 degrees. Therefore, it is impossible for a quadrilateral to have all four angles as obtuse.
7. Final Answer:
The statement is False (F).
A quadrilateral is a polygon with four sides and four angles.
The sum of the internal angles of any quadrilateral is always 360 degrees. This can be derived from the fact that a quadrilateral can be divided into two triangles, each having a sum of angles equal to 180 degrees. Therefore, 180+180=360 degrees.
An obtuse angle is an angle that is greater than 90 degrees but less than 180 degrees.
If we assume that all four angles of the quadrilateral are obtuse, we can denote them as:
- Angle A > 90 degrees
- Angle B > 90 degrees
- Angle C > 90 degrees
- Angle D > 90 degrees
If each angle is greater than 90 degrees, we can express this mathematically:
Angle A+Angle B+Angle C+Angle D>90+90+90+90=360 degrees
Since the sum of the angles exceeds 360 degrees when all angles are obtuse, it contradicts the fundamental property of quadrilaterals where the sum must equal 360 degrees. Therefore, it is impossible for a quadrilateral to have all four angles as obtuse.
The statement is False (F).
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
A quadrilateral can be drawn if all four sides and one angle is known.
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral can be drawn if all four sides and one diagonal is known.
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral can be drawn when all the four angles and one side is given.
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral has two diagonals.
View SolutionState whether the statements are true (T) or (F) false.
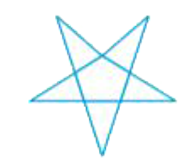 is a polygon.
is a polygon.
View SolutionState whether the statements are true or falsea−b=b−a
View SolutionState whether the statements are true or falsea×b=b×a
View SolutionState whether the statements are true or falsea÷a=b÷a
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral can be drawn if only measures of four sides are given.
View SolutionState whether the statements are true (T) or (F) false.
All squares are rectangles.
View Solution
