State whether the statements are true (T) or (F) false.
A quadrilateral can be constructed uniquely if three angles and any two sides are given..
To determine whether the statement "A quadrilateral can be constructed uniquely if three angles and any two sides are given" is true or false, we can follow these steps:
Step 1: Understand the properties of a quadrilateral
A quadrilateral is a four-sided polygon, and the sum of its interior angles is always 360 degrees.
Step 2: Analyze the given information
We are given three angles and two sides of a quadrilateral. Let's denote the angles as A, B, C, and D, where D is the angle we need to find.
Step 3: Calculate the fourth angle
Since the sum of all angles in a quadrilateral is 360 degrees, we can find the fourth angle (D) using the formula:
D=360−(A+B+C)
Step 4: Determine the number of sides and angles
In total, we have:
- 4 angles (A, B, C, D)
- 2 sides
Step 5: Assess the uniqueness of the quadrilateral
With the three angles known, we can calculate the fourth angle. Thus, we have:
- 2 sides
- 4 angles
In general, a quadrilateral can be constructed uniquely if the number of sides is greater than the number of angles. In this case, we have 2 sides and 4 angles, which means we can construct a quadrilateral uniquely.
Conclusion
The statement is True (T). A quadrilateral can indeed be constructed uniquely if three angles and any two sides are given.
---
A quadrilateral is a four-sided polygon, and the sum of its interior angles is always 360 degrees.
We are given three angles and two sides of a quadrilateral. Let's denote the angles as A, B, C, and D, where D is the angle we need to find.
Since the sum of all angles in a quadrilateral is 360 degrees, we can find the fourth angle (D) using the formula:
D=360−(A+B+C)
In total, we have:
- 4 angles (A, B, C, D)
- 2 sides
With the three angles known, we can calculate the fourth angle. Thus, we have:
- 2 sides
- 4 angles
The statement is True (T). A quadrilateral can indeed be constructed uniquely if three angles and any two sides are given.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
A quadrilateral has two diagonals.
View SolutionState whether the statements are true (T) or (F) false.
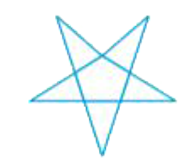 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
A rhombus can be constructed uniquely if both diagonals are given.
View SolutionState whether the statements are true (T) or (F) false.
All squares are rectangles.
View SolutionA quadrilateral can be constructed uniquely if its three sides and __________ angles are given.
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View SolutionState whether the statements are true (T) or (F) false.
A parallelogram can be constructed uniquely if both diagonals and the angle between them is given.
View SolutionState whether the statements are true (T) or (F) false.
 is a concave pentagon.
is a concave pentagon.
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral can have all four angles as obtuse.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a trapezium.
View Solution
