The vertices A, B, C and D of a quadrilateral ABCD lie on a circle. ∠A is thrice ∠C and ∠D is twice ∠B. What is the difference between the measures of ∠B and ∠C?
किसी चतुर्भुज ABCD के शीर्ष बिंदु A, B, C और D एक वृत्त पर स्थित हैं | कोण A कोण C से तिगुना है तथा कोण D कोण B से दोगुना है | कोण B और कोण C के मान में क्या अंतर है ?
15∘
28∘
18∘
20∘
To solve the problem, we need to find the difference between the measures of angle B and angle C in the cyclic quadrilateral ABCD, given the relationships between the angles.
1. Understanding the properties of a cyclic quadrilateral:
In a cyclic quadrilateral, the sum of the opposite angles is equal to 180 degrees. Therefore, we have:
- ∠A+∠C=180∘ (1)
- ∠B+∠D=180∘ (2)
2. Setting up the relationships given in the problem:
We are given that:
- ∠A=3×∠C (3)
- ∠D=2×∠B (4)
3. Substituting equation (3) into equation (1):
From (3), we can express ∠A in terms of ∠C:
∠A=3∠C
Substituting this into (1):
3∠C+∠C=180∘
Simplifying gives:
4∠C=180∘
Therefore:
∠C=180∘4=45∘
4. Finding angle A:
Now that we have ∠C, we can find ∠A:
∠A=3×45∘=135∘
5. Using equation (2) to find angle B and angle D:
We know from (2):
∠B+∠D=180∘
From (4), we can express ∠D in terms of ∠B:
∠D=2∠B
Substituting this into (2):
∠B+2∠B=180∘
Simplifying gives:
3∠B=180∘
Therefore:
∠B=180∘3=60∘
6. Finding the difference between angle B and angle C:
Now we can find the difference between ∠B and ∠C:
Difference=∠B−∠C=60∘−45∘=15∘
Final Answer:
The difference between the measures of angle B and angle C is 15∘.
In a cyclic quadrilateral, the sum of the opposite angles is equal to 180 degrees. Therefore, we have:
- ∠A+∠C=180∘ (1)
- ∠B+∠D=180∘ (2)
We are given that:
- ∠A=3×∠C (3)
- ∠D=2×∠B (4)
From (3), we can express ∠A in terms of ∠C:
∠A=3∠C
Substituting this into (1):
3∠C+∠C=180∘
Simplifying gives:
4∠C=180∘
Therefore:
∠C=180∘4=45∘
Now that we have ∠C, we can find ∠A:
∠A=3×45∘=135∘
We know from (2):
∠B+∠D=180∘
From (4), we can express ∠D in terms of ∠B:
∠D=2∠B
Substituting this into (2):
∠B+2∠B=180∘
Simplifying gives:
3∠B=180∘
Therefore:
∠B=180∘3=60∘
Now we can find the difference between ∠B and ∠C:
Difference=∠B−∠C=60∘−45∘=15∘
The difference between the measures of angle B and angle C is 15∘.
Topper's Solved these Questions
Similar Questions
The vertices A, B, C, and D of a quadrilateral ABCD lie on a circle. ∠A is thrice ∠Cand∠D is twice ∠B. What is the difference between the measures of ∠Band∠C?
किसी परम भुज ABCDके शीर्ष A, B, C,और D एक वृत्त पर स्थित है| ∠A , ∠C का तिगुना है और ∠D, ∠B का दोगुना है| angle B और angle C के माप मेँ कया अंतर है ?
View SolutionABCD is a cyclic quadrilateral in which ∠A=67∘ and ∠B=92∘. What is the difference between the measure of ∠C and ∠D ?
ABCD एक चक्रीय चतुर्भुज है जिसमें ∠A=67∘ और ∠B=92∘ है | ∠C और ∠D के माप में क्या अंतर है ?
View Solution
Knowledge Check
Angle 'A' of the quadrilateral ABCD is 26∘ less than angle B. Angle B is twice angle C and angle C is 10∘ more than the angle D. What would be the measure of angle A?
A104∘B126∘C56∘D106∘If angles A, B, C and D of the quadrilateral ABCD, taken in order are in the ratio 3 : 7 : 6 : 4, then ABCD is a
ArhombusBparallelogramCtrapeziumDkiteIn a quadrilateral ABCD, ∠A:∠B:∠C:∠D=3:4:5:6. Then ABCD is a __________
ATrapeziumBParallelogramCRhombusDKite
In parallelogram ABCD, find ∠B, ∠C and ∠D.
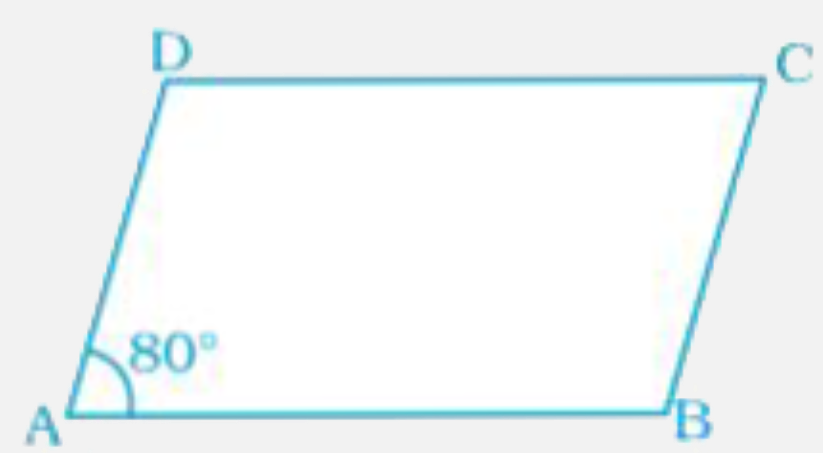
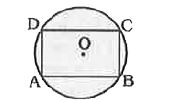
View SolutionIna cyclic quadrilateral
∠A+∠C=∠B+∠D=?
View SolutionThe angles A, B,C, D of a quadrilateral ABCD are in the ratio 1:2:4:5.
What is cos (A + B) equal to ?
View SolutionPQRS is a cyclic quadrilateral. If angle P is three times the angle R and angle S is five times the angle Q , then the sum of angles Q and R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R का तिगुना है तथा कोण S कोण Q से पांच गुना है, तो कोण Q और R का योग ज्ञात करें |
View SolutionIf angles A, B, C and D of the quadrilateral ABCD, taken in order are in the ratio 3 : 7 : 6 : 4, then ABCD is a
View Solution
