Question

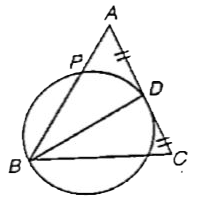
In $\angle ABC$, AB=AC . A circle drawn through B touches AC at D and intersects AB at P. If D is the mid point of AC and AP = 2.5 cm, then AB is equal to:

त्रिभुज ABC में, AB = AC है | B से खींचा गया एक वृत्त AC को D पर स्पर्श करता है तथा AB को P पर
काटता है | यदि D, AC का मध्य बिंदु है एवं AP = 2.5 सेमी है, तो AB का मान किसके बराबर है ?

Options

A. 9 cm
B. 7.5 cm
C. 12.5 cm
D. 10 cm

Explanation

To solve the problem step by step, we will use the properties of triangles and circles, particularly focusing on the relationships between the segments defined in the problem.

1. Identify the Given Information:
- In triangle ABC, we have AB = AC.
- A circle drawn through point B touches line AC at point D and intersects line AB at point P.
- D is the midpoint of AC.
- AP = 2.5 cm.

2. Define the Lengths:
- Since D is the midpoint of AC, we can denote the lengths as follows:
- Let AD = DC = x.
- Therefore, AC = AD + DC = x + x = 2x.

3. Use the Tangent-Secant Theorem:
- According to the tangent-secant theorem, we know that:
\( AD^2 = AP \times AB \)
- Substituting the known values:
\( x^2 = 2.5 \times AB \)

4. Express AB in Terms of x:
- Since we also have AC = 2x, and we know AB = AC, we can write:
\( AB = 2x \)
- Now substituting this into the equation from the tangent-secant theorem:
\( x^2 = 2.5 \times (2x) \)
- Simplifying gives:
\( x^2 = 5x \)

5. Rearranging the Equation:
- Rearranging the equation:
\( x^2 - 5x = 0 \)
- Factoring out x:
\( x(x - 5) = 0 \)
- This gives us two solutions: x = 0 or x = 5. Since x represents a length, we take x = 5.

6. Calculate AB:
- Now substituting back to find AB:
\( AB = 2x = 2 \times 5 = 10 \text{ cm} \)

Final Answer:
AB = 10 cm.