A steel wire of length 1m and mass 0.1kg and having a uniform cross-sectional area of 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 20∘C. If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Ysteel=2×1011N/m2,αsteel=1.21×10−5/.∘C).Solution in Gujrati
The correct Answer is:11 Hz
For wire, ΔL=Lαθ=FLAY⇒D=AYαθ
∴f=12L√Fμ=12×1√10−6×2×1011×1.21×105×200.1
=11Hz
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
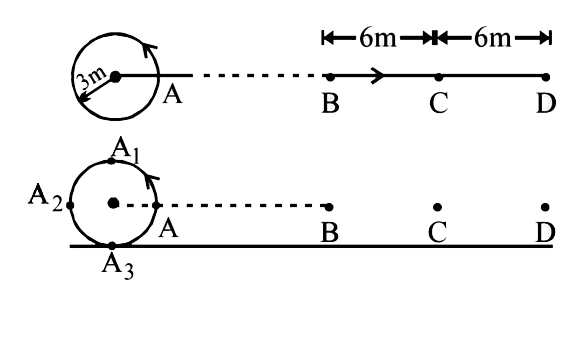
A source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionTube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionStatement-1 : Sound travels faster in moist air
Statement-2 : The density of moist air is less then density of dry air.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA steel wire of length 1m , mass 0.1kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If transverse calculate the frequency of the fundamental mode of vibration. Given for steel Y = 2 xx 10^(11)N//m^(2) alpha = 1.21 xx 10^(-5) per ^(@)C
View SolutionA steel wire is rigidly fixed at both ends its length mass and cross sectional area are 1m, 0.1 kg and 106m2 respectively then the temperature of the wire is lowered by 20∘C if the transverse waves are setup by plucking the wire at 0.25m from one end and assuming that wire vibrates with minimum number of loops possible for such a case. Find the frequency of vibration (in Hz). [coefficient of linear expansion of steel =1.21×10−6/.∘C and young's modulus =2×1011/N/m2]
View SolutionA steel wire of length 1 m and mass 0.1 kg and having a uniform cross-sectional area of 10^(-6) m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Y_(steel)=2xx 10^(11) N//m^(2),alpha_(steel)=1.21 xx 10^(-5)//.^(@)C) .
View SolutionThe area of cross section of a steel wire (Y=2.0×1011N/m2) is 0.1cm2. The force required to double is length will be
View SolutionA body of mass 1 kg is fastened to one end of a steel wire of cross- section area 3 xx 10^(-6)m^(2) and is rotated in horizantal circle of radius 20 cm with a constant speed 2 m//s . Find the elongation of the wire (Y= 2 xx 10^(11) N//m^(2))
View SolutionA fine steel wire of length 4m is fixed rigidly in a heavy brass frame as ashown in figure . It is just taut at 20∘C. The tensile stress developed in steel wire it whole system is heated to 120∘C is :-
(Givenαbrass=1.8×10−5.∘C−1,αsteel=1.2×10−5.∘C,Ysteel=2×1011Nm−2,Ybrass=1.7×107Nm−2)
_S01_081_Q01.png)
View SolutionA steel wire having cross-sectional area 1.5 mm^(2) when stretched by a load produces a lateral strain 1.5 xx 10^(-5) . Calculate the mass attached to the wire. ( Y_("steel") = 2xx 10^(11) N//m^(2) , Poisson's ration sigma = 0.291, g = 9.8 m//s^(2) )
View SolutionAn aluminium wire and a steel wire of the same length and cross section are joined end to end. The composite wire is hung from a rigid support and the load is suspended at the free end. If Y_(AL) = 7xx10^(10) N//m^(2) and Y_("steel") = 7xx10^(11) N//m^(2) , the ratio of elongation of aluminium and steel wires is
View SolutionA steel wire of length 0.20m and uniform cross section 10^(-6)m^(2) is tied rigidly at both ends. The temperature of the wire is changed from 40^(@) C to 20^(@)C . Calculate the thermal tension in the wire given alpha =1.1. xx 10^(-5)//.^(@)C and Y=2xx10^(11)Nm^(-2)
View SolutionA steel wire of length 1 m, mass 0.1 kg and uniform cross sectional area 10^(-6)m^(2) is rigidly fixed at two ends. The temperature of the wire is lowered by 20^(@) C . If transverse waves are now set up by lucking the string at the middle, calculate the frequency of the fundamental tone. Givne, for steel, co-efficient of linear expansion = 1.21 xx 10^(-5_(@))C^(1) and Young's modulus = 2 xx 10 ^(11) N* m^(-2) .
View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 200C. If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2×1011N/m2andα=1.21×10−5l0C]
View SolutionThe uniform transverse cut area of a steel wire of length 1m and mass 0.1 kg 10^(-6)m^(2) is. Is tightly tightened. Wire temperature 20^(@)C Let's reduce it. If the wire vibrates in its core, find the frequency (in hertz) Y_("steel")=2xx10^(11)N//m^(2), alpha_("steel")=1.21xx10^(-5)//""^(@)C Take)
View Solution
