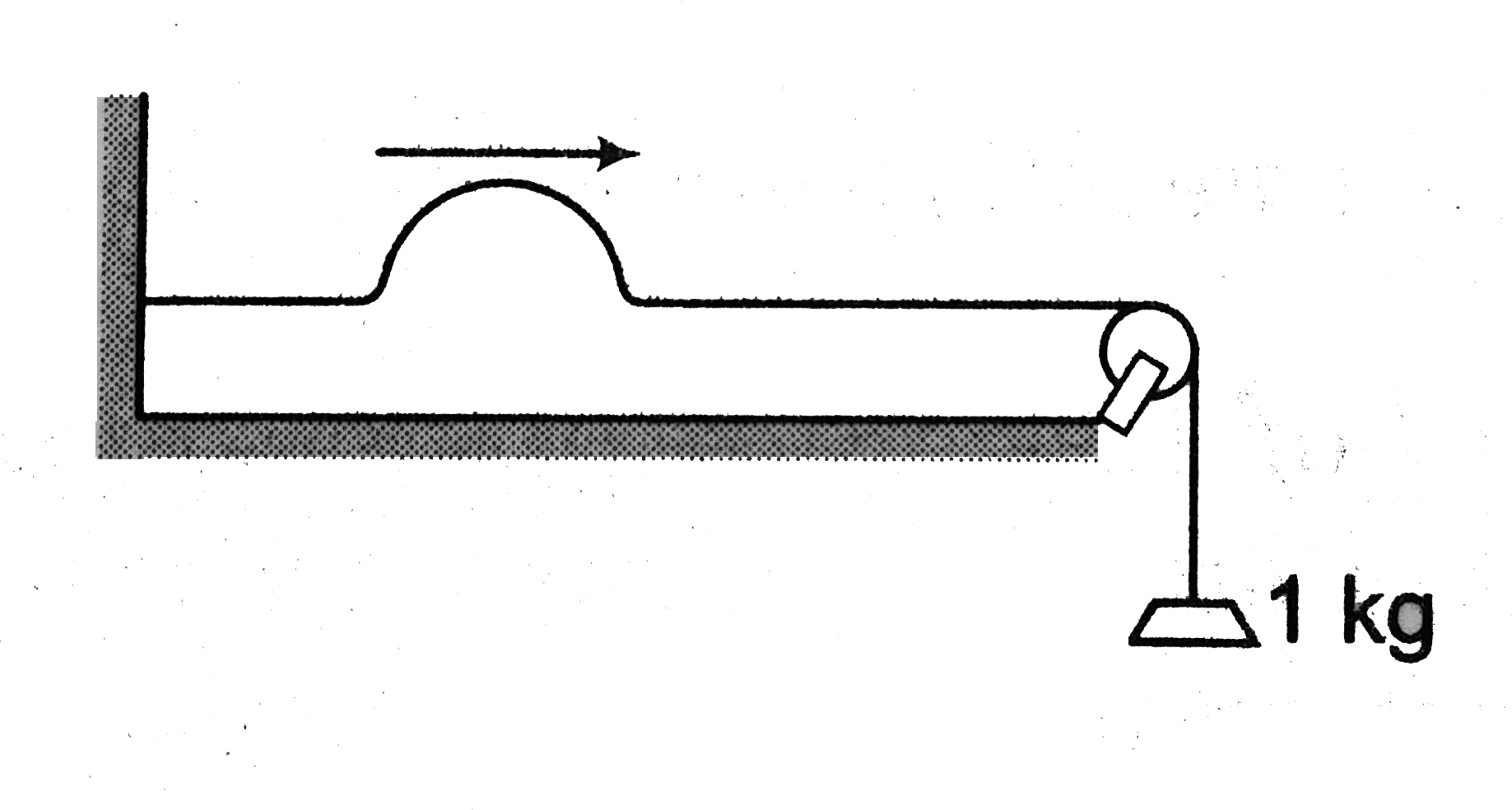
Figure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:0.05s
v=√1×1010−3/10−2=10m/s,t=Lv=0.510=0.05sec
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
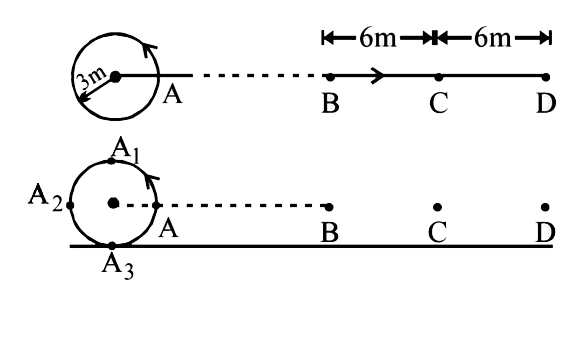
A source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionTube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionStatement-1 : Sound travels faster in moist air
Statement-2 : The density of moist air is less then density of dry air.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionA 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.
View SolutionA heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60cms−1 on the string when the car is at rest and 62cms−1 when the car accelerates on a horizontal road. Find the acceleration of the car. Take g=10ms−2
View SolutionThe pulse shown in figure has a speed of 10cm/s .

(a) If the linear mass density of the right string is 0.25 that of the left string, at what speed does the transmitted pulse travel?
(b) Compare the heights of the transmitted pulse and the reflected pulse to that of the incident pulse.
View SolutionTwo pulses travel in mutually opposite directions in a string with a speed of 2.5cm/s as shown in the figure. Initially the pulses are 10cm apart. What will be the state of the string after two seconds?
View SolutionA wave pulse is travelling on a string of linear mass density 10gcm^(-1) under a tension of 1kg wt. Calculate the time taken by the pulse to travel a distance of 50cm on the string. Take g=10m//s^(2).
View SolutionA wave pulse is travelling on a string of linear mass density 1.0gcm−1 under a tension of 1 kg wt. Calculate the time taken by the pulse to travel a distance of 50 cm on the string.Given g=10ms−2.
View SolutionA way pulse is travelling on a string of linear mass density 6.4 xx 10^(-3)kg m^(-1) under a load of 80 kgf . Calculate the time taken by the pulse to traverse the string, if its length is 0.7 m .
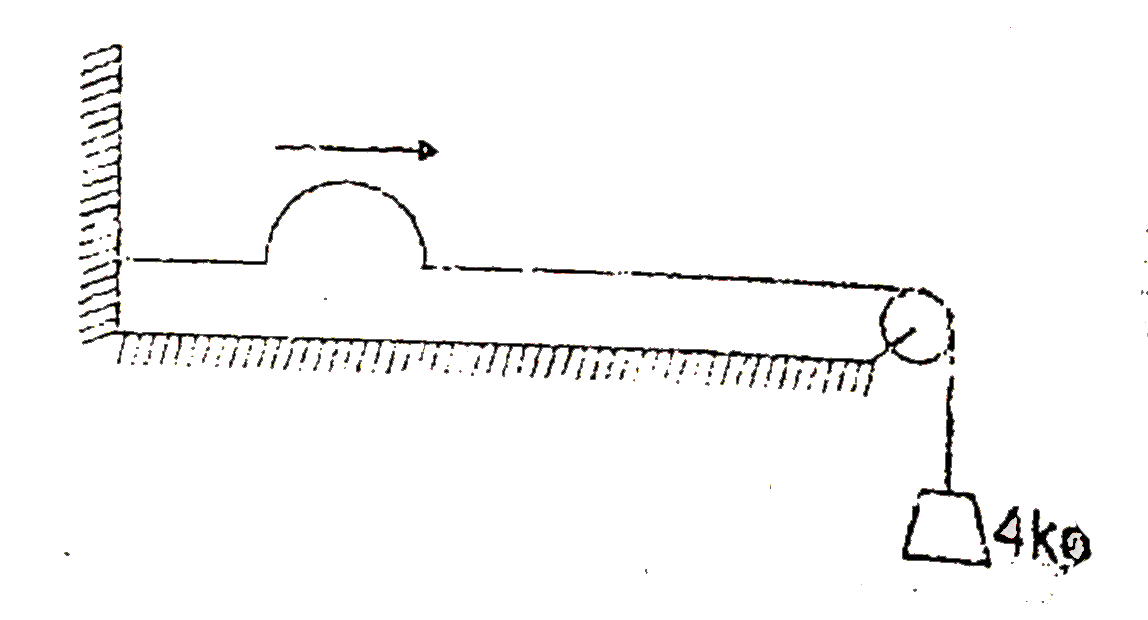
View SolutionFigure shows a string of linear mass density 1.0g/cm on which a wave pulse is travelling. Find the time taken (in milli second) by the pulse in travelling through a distance of 60cm on the string. Take g=10m/s2.
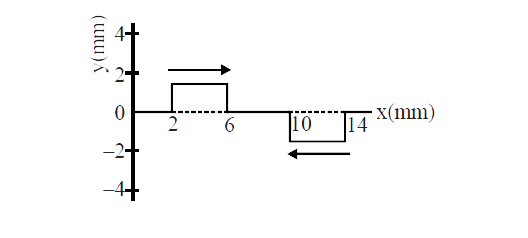
View SolutionFollowing figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionA 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass desity of 19.2×10−3kgm−1. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elavator accelerates up at the rate of 2.0ms−2.Takeg=10ms−2.
View Solution
