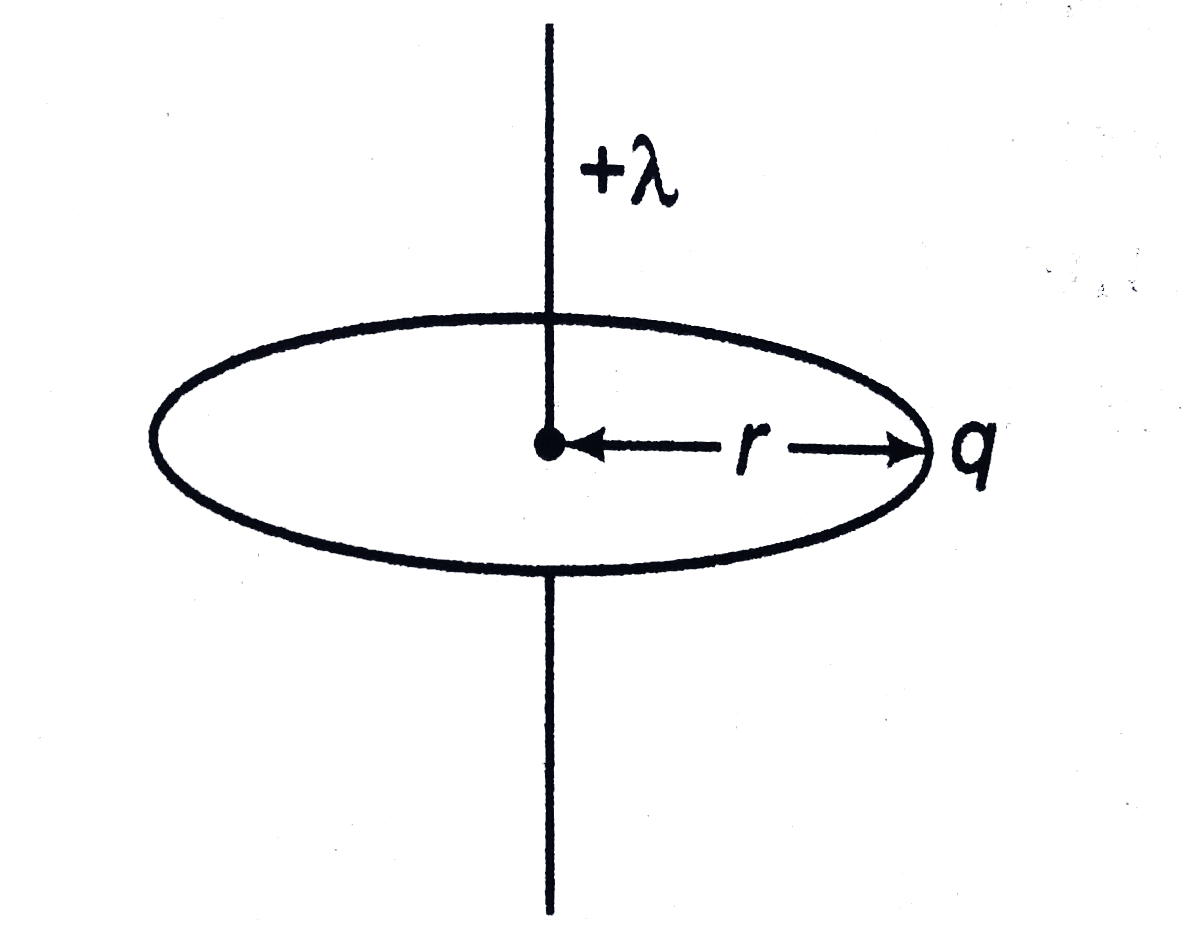
A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
 where , k=14πε0)Solution in Gujrati
where , k=14πε0)Solution in Gujrati
T=2πr√m2kλq
T2=4π2m2kλqr3
T=12πr√2kλqm
T=12πr√m2kλq
The correct Answer is:A
We have centripetal force equation
q(2kγr)=mv2r
so v=√2kqγm Now T=2πrv=2πr√m2kγq
where, k=14πε0
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHS
1 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA quantity of 2 mole of helium gas undergoes a thermodynamic process, in which molar specific heat capacity of the gas depends on absolute temperatureT , according to relation:
C=3RT4T0
where T0 is initial temperature of gas. It is observed that when temperature is increased. volume of gas first decrease then increase. The total work done on the gas until it reaches minimum volume is :-
View SolutionIf complex number z(z≠2) satisfies the equation z2=4z+|z|2+16|z|3, then what is the value of |z|4 ?
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
 where , k=14πε0)
where , k=14πε0)
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA charge particle moves in a circle around an infinite line charge with the center of circle at the line and line being perpendicular to the plane of circle. Let r be the radius of circle. The velocity of the particle depends upon which power of r.
View SolutionTwo infinitely long line charges having charge density lamda each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and lamda q gt 0 Neglect gravity. Find the time period.
View Solutionअति लम्बे आवेशित तार के गुर्द q आवेशयुक्त द्रव्यमान m का एक कण r त्रिज्या के वृत्तीय पथ एक एकसमान चाल v से चक्कर लगा रहा है। यदि तार पर आवेश का रैखिक घनत्व (linear dnesity of charge ) λ हो, तब
View SolutionAn electron is moving around infinite linear positive charge in the orbit of 0.1 m. If the linear charge density is 1μC/m, the velocity of electron will be
View SolutionA particle of charge -q and mass m moves in a circle aroung a long wire of linear charge density λ. If r = radius of the circular path and T = time period of the motion circular path. Then :
View SolutionA particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
View SolutionA particle of charge -q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +lamda . Then, time period will be where , k=1/4piepsilon_0)
View SolutionIntensity of electric field at a perpendicular distance of 0.5 m from an infinitely long line charge having linear charge density (lamda) is 3.6 xx 10^(3) Vm^(-1) . Find the value of lamda
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View Solution
